
【题目】下面我们做一次折叠活动: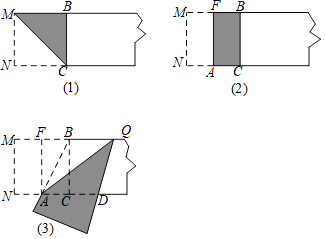
第一步,在一张宽为2的矩形纸片的一端,利用图(1)的方法折出一个正方形,然后把纸片展平,折痕为MC;
第二步,如图(2),把这个正方形折成两个相等的矩形,再把纸片展平,折痕为FA;
第三步,折出内侧矩形FACB的对角线AB,并将AB折到图(3)中所示的AD处,折痕为AQ.
根据以上的操作过程,完成下列问题:
(1)求CD的长.
(2)请判断四边形ABQD的形状,并说明你的理由.
【答案】
(1)解:∵∠M=∠N=∠MBC=90°,
∴四边形MNCB是矩形,
∵MB=MN=2,
∴矩形MNCB是正方形,
∴NC=CB=2,
由折叠得:AN=AC= ![]() NC=1,
NC=1,
Rt△ACB中,由勾股定理得:AB= ![]() =
= ![]() ,
,
∴AD=AB= ![]() ,
,
∴CD=AD﹣AC= ![]() ﹣1;
﹣1;
(2)解:四边形ABQD是菱形,理由是:
由折叠得:AB=AD,∠BAQ=∠QAD,
∵BQ∥AD,
∴∠BQA=∠QAD,
∴∠BAQ=∠BQA,
∴AB=BQ,
∴BQ=AD,BQ∥AD,
∴四边形ABQD是平行四边形,
∵AB=AD,
∴四边形ABQD是菱形.
【解析】(1)首先证明四边形MNCB为正方形,然后再依据折叠的性质得到:CA=1,AB=AD,最后再依据CD=AD-AC求解即可;
(2)根据平行线的性质和折叠的性质可得到∠BAQ=∠BQA,然后依据等角对等边的性质得到AB=BQ,接下来,依据一组对边平行且相等的四边形为平行四边形可证明四边形ABQD是平行四边形,再由AB=AD,可得四边形ABQD是菱形.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
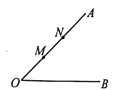
【题目】如图,∠AOB=45°,点M、N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P、M、N构成等腰三角形的点P恰好有三个,则x的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线AB:y= ![]() x+4交x轴于点A,交y轴于点B.直线CD:y=﹣
x+4交x轴于点A,交y轴于点B.直线CD:y=﹣ ![]() x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.
x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.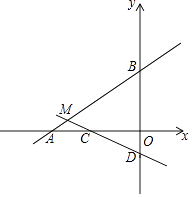
(1)直接写出点B和点D的坐标;
(2)若点P是射线MD上的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系;
(3)当S=20时,平面直角坐标系内是否存在点E,使以点B、E、P、M为顶点的四边形是平行四边形?若存在,请直接写出所有符合条件的点E的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度,密度k(辆/千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量q与速度v之间关系的部分数据如下表:

(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是 (只填上正确答案的序号)
①q=90v+100;②q=![]() ;③
;③![]() .
.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足q=vk,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当12≤v<18时道路出现轻度拥堵.试分析当车流密度k在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年下半年开始,不同品牌的共享单车出现在城市的大街小巷.现已知A品牌共享单车计费方式为:初始骑行单价为1元/半小时,不足半小时按半小时计算.内设邀请机制,每邀请一位好友注册认证并充值押金成功,双方骑行单价均降价0.1元/半小时,骑行单价最低可降至0.1元/半小时(比如,某用户邀请了3位好友,则骑行单价为0.7元/半小时).B品牌共享单车计费方式为:0.5元/半小时,不足半小时按半小时计算.
(1)某用户准备选择A品牌共享单车使用,设该用户邀请好友x名(x为整数,x≥0),该用户的骑行单价为y元/半小时.请写出y关于x的函数解析式.
(2)若有A,B两种品牌的共享单车各一辆供某用户一人选择使用,请你根据该用户已邀请好友的人数,给出经济实惠的选择建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:探究函数y=|x|﹣2的图象与性质.
小华根据学习函数的经验,对函数y=|x|﹣2的图象与性质进行了探究.
下面是小华的探究过程,请补充完整:
(1)在函数y=|x|﹣2中,自变量x可以是任意实数;
如表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m=;
②若A(n,8),B(10,8)为该函数图象上不同的两点,则n=;
(2)①如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;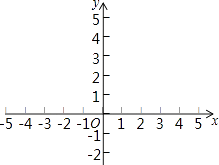
(3)该函数的最小值为;
(4)已知直线 ![]() 与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .
与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com