
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度,密度k(辆/千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量q与速度v之间关系的部分数据如下表:

(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是 (只填上正确答案的序号)
①q=90v+100;②q=![]() ;③
;③![]() .
.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足q=vk,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当12≤v<18时道路出现轻度拥堵.试分析当车流密度k在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值.
【答案】(1)③;(2)v=30时,q达到最大值,q的最大值为1800;(3)①84<k≤96;②流量q最大时d的值为60.
【解析】
试题分析:(1)利用函数的增减性即可判断;
(2)利用配方法,根据二次函数的性质即可解决问题;
(3)①求出v=12或18时,定义的k的值即可解决问题;
②由题意流量q最大时d的值=流量q最大时k的值;
试题解析:(1)函数①q=90v+100,q随v的增大而增大,显然不符合题意.
函数②q=![]() q随v的增大而减小,显然不符合题意.
q随v的增大而减小,显然不符合题意.
故刻画q,v关系最准确的是③.
故答案为:③.
(2)∵![]() =
=![]() ,∵﹣2<0,∴v=30时,q达到最大值,q的最大值为1800.
,∵﹣2<0,∴v=30时,q达到最大值,q的最大值为1800.
(3)①当v=12时,q=1152,此时k=96,当v=18时,q=1512,此时k=84,∴84<k≤96.
②当v=30时,q=1800,此时k=60,∵在理想状态下,假设前后两车车头之间的距离d(米)均相等,∴流量q最大时d的值为60.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如果x<0,y>0,x+y<0,那么下列关系式中正确的是( )
A.x>y>﹣y>﹣x
B.﹣x>y>﹣y>x
C.y>﹣x>﹣y>x
D.﹣x>y>x>﹣y
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面我们做一次折叠活动: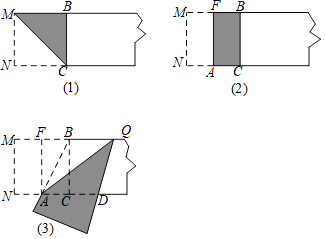
第一步,在一张宽为2的矩形纸片的一端,利用图(1)的方法折出一个正方形,然后把纸片展平,折痕为MC;
第二步,如图(2),把这个正方形折成两个相等的矩形,再把纸片展平,折痕为FA;
第三步,折出内侧矩形FACB的对角线AB,并将AB折到图(3)中所示的AD处,折痕为AQ.
根据以上的操作过程,完成下列问题:
(1)求CD的长.
(2)请判断四边形ABQD的形状,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一节期间,电器市场火爆,某商店需要购进一批电视机和洗衣机,根据市场调查,电视机与洗衣机的进价和售价如下表:
类别 | 电视机 | 洗衣机 |
进价(元/台) | 1800 | 1500 |
售价(元/台) | 2000 | 1600 |
若该商店计划电视机和洗衣机共100台,设购进电视机x台,获得的总利润y元.
(1)求出y与x的函数关系;
(2)已知商店最多筹集资金161800元,求购进多少台电视机,才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最多利润.(利润=售价﹣进价)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com