
【题目】五一节期间,电器市场火爆,某商店需要购进一批电视机和洗衣机,根据市场调查,电视机与洗衣机的进价和售价如下表:
类别 | 电视机 | 洗衣机 |
进价(元/台) | 1800 | 1500 |
售价(元/台) | 2000 | 1600 |
若该商店计划电视机和洗衣机共100台,设购进电视机x台,获得的总利润y元.
(1)求出y与x的函数关系;
(2)已知商店最多筹集资金161800元,求购进多少台电视机,才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最多利润.(利润=售价﹣进价)
【答案】
(1)解:y=(2000﹣1800)x+(1600﹣1500)(100﹣x)=100x+10000
(2)解:依题意得,1800x+1500(100﹣x)≤161800,
解得,x≤39 ![]() ,
,
∵x是整数,
∴x的最大值是39.
∵y=100x+10000中,k=100>0,
∴y随x的增大而增大,
∴当x=39时,y有最大值,最大值是:100×39+10000=13900(元).
【解析】(1)根据总利润=一台电视机的利润×电视机的销售量+一台洗衣机的利润×洗衣机的销售量列出解析式即可;
(2)首先依据商店最多筹集资金161800元列出不等式,然后求得不等式的解集,最后,再根据一次函数的性质可得到获利最多的方案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度,密度k(辆/千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量q与速度v之间关系的部分数据如下表:

(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是 (只填上正确答案的序号)
①q=90v+100;②q=![]() ;③
;③![]() .
.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足q=vk,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当12≤v<18时道路出现轻度拥堵.试分析当车流密度k在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
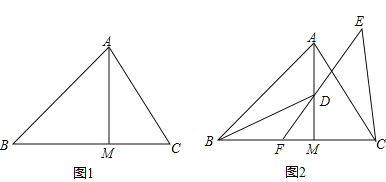
【题目】在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.
(1)如图1,若AB=3![]() ,BC=5,求AC的长;
,BC=5,求AC的长;
(2)如图2,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:探究函数y=|x|﹣2的图象与性质.
小华根据学习函数的经验,对函数y=|x|﹣2的图象与性质进行了探究.
下面是小华的探究过程,请补充完整:
(1)在函数y=|x|﹣2中,自变量x可以是任意实数;
如表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m=;
②若A(n,8),B(10,8)为该函数图象上不同的两点,则n=;
(2)①如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;
(3)该函数的最小值为;
(4)已知直线 ![]() 与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .
与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com