
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ֱ֪��AB��y= ![]() x+4��x���ڵ�A����y���ڵ�B��ֱ��CD��y=��
x+4��x���ڵ�A����y���ڵ�B��ֱ��CD��y=�� ![]() x��1��ֱ��AB�ཻ�ڵ�M����x���ڵ�C����y���ڵ�D��
x��1��ֱ��AB�ཻ�ڵ�M����x���ڵ�C����y���ڵ�D��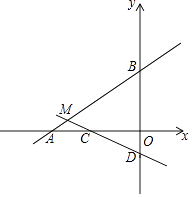
��1��ֱ��д����B�͵�D�����ꣻ
��2������P������MD�ϵ�һ�����㣬���P�ĺ�������x����PBM�������S����S��x֮��ĺ�����ϵ��
��3����S=20ʱ��ƽ��ֱ������ϵ���Ƿ���ڵ�E��ʹ�Ե�B��E��P��MΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�����з��������ĵ�E�����ꣻ�������ڣ�˵�����ɣ�
���𰸡�
��1���⣺�ߵ�B��ֱ��AB��y= ![]() x+4��y��Ľ������꣬
x+4��y��Ľ������꣬
��B��0��4����
�ߵ�D��ֱ��CD��y=�� ![]() x��1��y��Ľ������꣬
x��1��y��Ľ������꣬
��D��0����1����
��2���⣺��ͼ1����ֱ��AB��CD�ཻ��M��
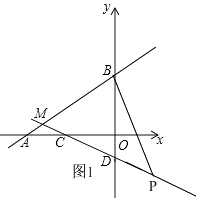
��M����5�� ![]() ����
����
�ߵ�P�ĺ�����Ϊx��
���P��x���� ![]() x��1����
x��1����
��B��0��4����D��0����1����
��BD=5��
�ߵ�P������MD�ϣ�����x��0ʱ��
S=S��BDM+S��BDP= ![]() ��5��5+x��=
��5��5+x��= ![]() x+
x+ ![]() ��
��
��3���⣺��ͼ���ɣ�1��֪��S= ![]() x+
x+ ![]() ��
��
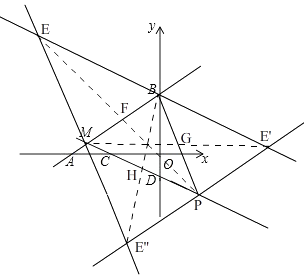
��S=20ʱ�� ![]() x+
x+ ![]() =20��
=20��
��x=3��
��P��3����2����
�ٵ�BP�ǶԽ���ʱ��ȡBP���е�G������MG���ӳ�ȡһ��E'ʹGE'=GE��
��E'��m��n����
��B��0��4����P��3����2����
��BP���е�����Ϊ�� ![]() ��1����
��1����
��M����5�� ![]() ����
����
�� ![]() =
= ![]() ��
�� ![]() =1��
=1��
��m=8��n= ![]() ��
��
��E'��8�� ![]() ����
����
�ڵ�ABΪ�Խ���ʱ��ͬ�ٵķ����ã�E����9��6����
�۵�MPΪ�Խ���ʱ��ͬ�ٵķ����ã�E'����2���� ![]() ����
����
�������������ĵ�E������Ϊ��8�� ![]() ��������9��6��������2����
��������9��6��������2���� ![]() ����
����
����������1����x=0���뺯������ʽ�õ���Ӧ��yֵ���Ӷ��ɵõ���B�͵�D�����ꣻ
��2�������������ε����תΪ��BDM�͡�BDP�����֮�ͣ�Ȼ�����������ε������ʽ�г�������ϵʽ���ɣ�
��3��������������öԽ�����ƽ�ֵ��ı�����ƽ���ı��κ��߶ε��е������ȷ���������ɵó�����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ħ�г���������8���ͣ���ʻʱÿСʱ����2�����ڲ����͵�����£���������Q����������ʻʱ��t��Сʱ��֮��ĺ�����ϵʽΪ________�������ʱ��t��ȡֵ��ΧΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㩁2a��a2��1���Ľ���ǣ� ��
A.��2a3��2a
B.��2a3+a
C.��2a3+2a
D.��a3+2a
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����n���ε�һ���������Խ��ߣ������n���ηֳ������εĸ����ǣ� ��
A. n�� B. (n-2) �� C. (n-3)�� D. ��n-1����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������һ���۵����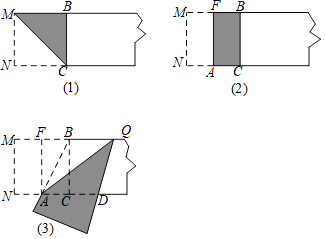
��һ������һ�ſ�Ϊ2�ľ���ֽƬ��һ�ˣ�����ͼ��1���ķ����۳�һ�������Σ�Ȼ���ֽƬչƽ���ۺ�ΪMC��
�ڶ�������ͼ��2����������������۳�������ȵľ��Σ��ٰ�ֽƬչƽ���ۺ�ΪFA��
���������۳��ڲ����FACB�ĶԽ���AB������AB�۵�ͼ��3������ʾ��AD�����ۺ�ΪAQ��
�������ϵIJ������̣�����������⣺
��1����CD�ij���
��2�����ж��ı���ABQD����״����˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С���ڳ�����ij�t��̨D������ý����ϵ��洬A�ĸ���Ϊ40��.��DE��3�ף�CE��2�ף�CEƽ���ڽ���AB��ӭˮ��BC���¶�i��1��0.75���³�BC��10�ף����ʱAB�ij�ԼΪ(�ο����ݣ�sin40����0.64��cos40����0.77��tan40����0.84)(����)

A. 5.1�� B. 6.3�� C. 7.1�� D. 9.2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com