
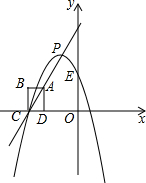
 ��ͼ����ƽ��ֱ������ϵ�У��߳�Ϊ1��������ABCD�Ķ���A��ֱ��y=2x+4�ϣ���B�ڵڶ����ޣ�C��D�������x���ϣ��ҵ�C�ڵ�D����࣬������y=-��x-m��2+n�Ķ���P��ֱ��y=2x+4���˶��������������߽�y���ڵ�E��
��ͼ����ƽ��ֱ������ϵ�У��߳�Ϊ1��������ABCD�Ķ���A��ֱ��y=2x+4�ϣ���B�ڵڶ����ޣ�C��D�������x���ϣ��ҵ�C�ڵ�D����࣬������y=-��x-m��2+n�Ķ���P��ֱ��y=2x+4���˶��������������߽�y���ڵ�E������ ��1���������εı߳�Ϊ1����õ�A�������꣬����A��������������y=2x+4����õ�A�ĺ����꣬�ɵ�A���������õ�C�����ꣻ
��2����������y=-��x-m��2+n�Ķ���P��ֱ��y=2x+4���˶����ɵõ�n=2m+4���ٽ���C��������������ߵĽ���ʽ�����m��n��ֵ���Ӷ�����������ߵĽ���ʽ��
��3����n��m�Ĺ�ϵ�ɽ������ߵĽ���ʽתΪy=-��x-m��2+2m+4��Ȼ��E�����꣨�ú�m��ʽ�ӱ�ʾ�����������������AC�Ľ���ʽ�����E���������AC�Ľ���ʽ�����m��ֵ��
��4����S��CDE=$\frac{1}{2}$DC•EO�ɵõ���CDE�������m�ĺ�����ϵʽ�����ݶ��κ����������Ժ͵�E��x���Ϸ������m��ȡֵ��Χ��
��� �⣺��1���������εı߳�Ϊ1��
���A��������Ϊ1��
�߽�y=1����y=2x+4�ã�2x+4=1����ã�x=-$\frac{3}{2}$��
��A��-$\frac{3}{2}$��1����
��D��-$\frac{3}{2}$��0��
��CD=1��
��C��$-\frac{5}{2}$��0��
��2����������y=-��x-m��2+n�Ķ���P��ֱ��y=2x+4���˶���
��n=2m+4��
�������ߵĽ���ʽΪy=-��x-m��2+2m+4��
�������߾�����C��-$\frac{5}{2}$��0����
�ࣨ-$\frac{5}{2}$-m��2+2m+4=0��
��ã�m1=m2=-$\frac{3}{2}$��
��n=2����-$\frac{3}{2}$��+4=1��
�������ߵĽ���ʽΪy=-��x+$\frac{3}{2}$��2+1��y=-x2-3x-$\frac{5}{4}$����
��3����������y=-��x-m��2+n�Ķ���P��ֱ��y=2x+4���˶���
��n=2m+4��
�������ߵĽ���ʽΪy=-��x-m��2+2m+4��
�߽�x=0����ã�y=-m2+2m+4��
��E��0��-m2+2m+4����
��ֱ��AC�Ľ���ʽΪy=kx+b��
�߽�A��-$\frac{3}{2}$��1��C��$-\frac{5}{2}$��0������ã�$\left\{\begin{array}{l}{-\frac{3}{2}k+b=1}\\{-\frac{5}{2}k+b=0}\end{array}\right.$�����k=1��b=$\frac{5}{2}$��
��ֱ��AC�Ľ���ʽΪy=x+$\frac{5}{2}$��
�ߵ�E��ֱ��AC�ϣ�
��-m2+2m+4=$\frac{5}{2}$��
��ã�m1=1-$\frac{\sqrt{10}}{2}$��m2=1+$\frac{\sqrt{10}}{2}$��
��4��S��CDE=$\frac{1}{2}$DC•EO=-$\frac{1}{2}$m2+m+2��
��m=-$\frac{b}{2a}$=1��a=-$\frac{1}{2}$��0��
�൱m��1ʱ��y��x�����������
��-$\frac{1}{2}$m2+m+2=0����ã�m1=1-$\sqrt{5}$��m2=1+$\sqrt{5}$����ȥ����
�ߵ�E��x����Ϸ���
��m��1-$\sqrt{5}$��
��m�ķ�Χ��1-$\sqrt{5}$��m��1��
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ������һ�κ��������κ����Ľ���ʽ�����κ�����ͼ�������ʣ����ݶ��κ�����������ȷ����m��ȡֵ��Χ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{7}{12}$ | C�� | $\frac{3}{4}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�O�У�AB���ң�����A�����߽�BO���ӳ����ڵ�C������O�İ뾶Ϊ3����C=20�㣬��$\widehat{AB}$�ij�Ϊ$\frac{11}{6}��$��
��ͼ���ڡ�O�У�AB���ң�����A�����߽�BO���ӳ����ڵ�C������O�İ뾶Ϊ3����C=20�㣬��$\widehat{AB}$�ij�Ϊ$\frac{11}{6}��$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
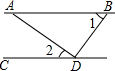 ��ͼ��AB��CD��AD��BD����1=55�㣬���2�Ĵ�С�ǣ�������
��ͼ��AB��CD��AD��BD����1=55�㣬���2�Ĵ�С�ǣ�������| A�� | 25�� | B�� | 30�� | C�� | 35�� | D�� | 40�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
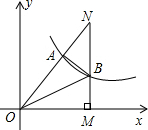 ��ͼ��˫����y=$\frac{k}{x}$��k��0������Rt��OMNб���ϵĵ�A����ֱ�DZ�MN�ཻ�ڵ�B����֪OA=2AN����OAB�����Ϊ10����k��ֵ��24��
��ͼ��˫����y=$\frac{k}{x}$��k��0������Rt��OMNб���ϵĵ�A����ֱ�DZ�MN�ཻ�ڵ�B����֪OA=2AN����OAB�����Ϊ10����k��ֵ��24���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��С���ڴ�¥30����PH=30�ף��Ĵ���P�����й۲⣬���ɽ����A���ĸ���Ϊ15�㣬ɽ�Ŵ��ĸ���Ϊ60�㣮��֪��ɽ�µ��¶�i����tan��ABC��Ϊ1��$\sqrt{3}$����P��H��B��C��A��ͬһ��ƽ���ϣ���H��B��C��ͬһ��ֱ���ϣ���PH�AHC����A��BC�ľ���Ϊ10$\sqrt{3}$�ף�
��ͼ��С���ڴ�¥30����PH=30�ף��Ĵ���P�����й۲⣬���ɽ����A���ĸ���Ϊ15�㣬ɽ�Ŵ��ĸ���Ϊ60�㣮��֪��ɽ�µ��¶�i����tan��ABC��Ϊ1��$\sqrt{3}$����P��H��B��C��A��ͬһ��ƽ���ϣ���H��B��C��ͬһ��ֱ���ϣ���PH�AHC����A��BC�ľ���Ϊ10$\sqrt{3}$�ף��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com