
【题目】如图,直线L:![]() 与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),线段OA上的动点M(与O,A不重合)从A点以每秒1个单位的速度沿x轴向左移动。
与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),线段OA上的动点M(与O,A不重合)从A点以每秒1个单位的速度沿x轴向左移动。

(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式,并写出t的取值范围;
(3)当t何值时△COM≌△AOB,并求此时M点的坐标。
【答案】(1)A(4,0)、B(0,2)
(2)当0<t<4时, S△OCM=8-2t;
(3)当t=2秒时△COM≌△AOB,此时M(2,0)
【解析】
(1)根据一次函数与x轴,y轴的交点坐标特点,即将x=0时;当y=0时代入函数解析式,即可求得A、B点的坐标.
(2)根据S△OCM=![]() ×OC·OM代值即可求得S与M的移动时间t之间的函数关系式,再根据M在线段OA上以每秒1个单位运动,且OA=4,即可求得t的取值范围
×OC·OM代值即可求得S与M的移动时间t之间的函数关系式,再根据M在线段OA上以每秒1个单位运动,且OA=4,即可求得t的取值范围
(3)根据在△COM和△AOB,已有OA=OC,∠AOB=∠COM,M在线段OA上,故可知OB=OM=2时,△COM≌△AOB,进而即可解题.
解:(1)对于直线AB:![]()
当x=0时,y=2;当y=0时,x=4
则A、B两点的坐标分别为A(4,0)、B(0,2)
(2)∵C(0,4),A(4,0)
∴OC=OA=4,
故M点在0<t<4时,OM=OA-AM=4-t,S△OCM=![]() ×4×(4-t)=8-2t;
×4×(4-t)=8-2t;
(3)∵当M在OA上,OA=OC
∴OB=OM=2时,△COM≌△AOB.
∴AM=OA-OM=4-2=2
∴动点M从A点以每秒1个单位的速度沿x轴向左移动2个单位,所需要的时间t=2秒钟,此时M(2,0),


科目:初中数学 来源: 题型:
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
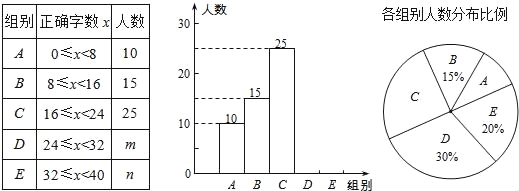
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某条道路上通行车辆限速60千米/时,道路的AB段为监测区,监测点P到AB的距离PH为50米(如图).已知点P在点A的北偏东45°方向上,且在点B的北偏西60°方向上,点B在点A的北偏东75°方向上,那么车辆通过AB段的时间在多少秒以内,可认定为超速?(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4).
≈1.4).
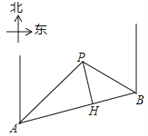
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=1,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.
(1)求点A的坐标和抛物线的表达式;
(2)当AE:EP=1:2时,求点E的坐标;
(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t的值.
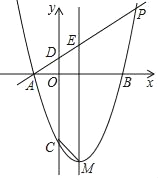
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中A(0,a)、B(b,0),且满足4(a﹣2)2+![]() (b﹣4)2=0,点P(m,m)在线段AB上
(b﹣4)2=0,点P(m,m)在线段AB上
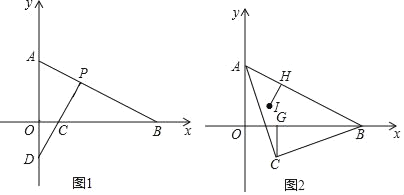
(1)求A、B的坐标;
(2)如图1,若过P作PC⊥AB交x轴于C,交y轴交于点D,求![]() 的值;
的值;
(3)如图2,以AB为斜边在AB下方作等腰直角△ABC,CG⊥OB于G,设I是∠OAB的角平分线与OP的交点,IH⊥AB于H.请探究![]() 的值是否发生改变,若不改变请求其值;若改变请说明理由.
的值是否发生改变,若不改变请求其值;若改变请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
(1)求从灯塔P看两轮船的视角(即∠APB)的度数?
(2)轮船C在∠APB的角平分线上,则轮船C在灯塔P的什么方位?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索发现:
(1)计算:当a 4, b 3时, a2 b2 ; (a b)(a b) 。
当a 1, b 2 时, a2 b2 ; (a b)(a b) 。
(2)你能从上面的计算中发现什么结论? 。
(3)利用你发现的结论,求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com