
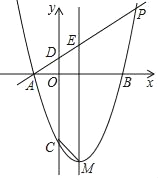
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=1,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.
(1)求点A的坐标和抛物线的表达式;
(2)当AE:EP=1:2时,求点E的坐标;
(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t的值.
【答案】(1)y=x2﹣2x﹣3;(2)E(1,4);(3)t=4.
【解析】分析:(1)依据抛物线的对称性可得到A、B的坐标,利用抛物线的交点式可得到抛物线的解析式;
(2)过点P作PF∥y轴,交x轴与点F,则△AEG∽△APF,从而可得到AF=6,然后可求得PF的长,从而可得到EG的长,故此可得到点E的坐标;
(3)先证明∠ADO=∠CME,然后,再求得点C和点M的坐标,从而可得到tan∠ADO=1,于是可得到OD=AO=1,故此可得到AP的解析式,最后求得直线AP与抛物线的交点坐标即可.
详解:(1)∵AB=4,抛物线y=x2+bx+c的对称轴为直线x=1,∴点A到对称轴的距离为2,∴A(﹣1,0),B(3,0),∴y=(x+1)(x﹣3)整理得:y=x2﹣2x﹣3;
(2)如下图所示:过点P作PF⊥x轴,垂足为F.
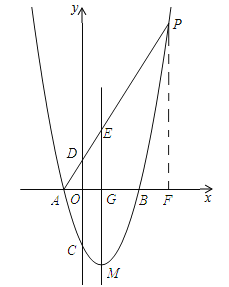
∵EG∥PF,AE:EP=1:2,∴![]() =
=![]() =
=![]() .
.
又∵AG=2,∴AF=6,∴F(5,0).
当x=5时,y=12,∴EG=4,∴E(1,4).
(3)∵CD∥EM,∴∠ADO=∠AEM.
又∵四边形CDEM是等腰梯形,∴∠ADO=∠CME,∴∠ADO=∠CME.
∵y=x2﹣2x﹣3,∴C(0,﹣3),M(1,﹣4)
∴tan∠DAO=tan∠CME=1,∴OA=OD=1,∴直线AP的解析式为y=x+1.
把y=x+1代入y=x2﹣2x﹣3得:x+1=x2﹣2x﹣3,解得:x=4或x=﹣1(舍去)
∴点P的横坐标为4,即t=4.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
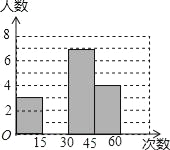
【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15≤x<30) | 6 | a |
第三组(30≤x<45) | 7 | 0.35 |
第四组(45≤x<60) | b | 0.20 |
(1)频数分布表中a=_____,b=_____,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,=,DE⊥BC,垂足为E.

(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若CE=1,AC=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=![]() ,BC=4.线段AB的垂直平分线DF分别交边AB、AC、BC所在的直线于点D、E、F.
,BC=4.线段AB的垂直平分线DF分别交边AB、AC、BC所在的直线于点D、E、F.
(1)求线段BF的长;
(2)求AE:EC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“清明小假期”举行促销活动,设立了一个可以自由转动的转盘进行摇奖活动,并规定顾客每购买200元商品,就可以获得一次转动转盘的机会,小明根据活动情况绘制了一个扇形统计图,如图所示.
(1)求每转动一次转盘所获得购物券金额的平均数;
(2)小明做了一次实验,他转了200次转盘,总共获得5800元购物券,他平均每转动一次转盘获得的购物券是多少元?
(3)请你说明上述两个结果为什么有差别?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L:![]() 与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),线段OA上的动点M(与O,A不重合)从A点以每秒1个单位的速度沿x轴向左移动。
与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),线段OA上的动点M(与O,A不重合)从A点以每秒1个单位的速度沿x轴向左移动。

(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式,并写出t的取值范围;
(3)当t何值时△COM≌△AOB,并求此时M点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
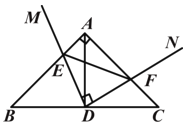
【题目】Rt△ ABC 中, AB=AC,点 D 为 BC 中点.∠ MDN=90°, ∠ MDN 绕点 D 旋转,DM、DN 分别与边 AB、AC 交于 E、F 两点.下列结论:① BE+CF=![]() BC;② S△AEF ≤
BC;② S△AEF ≤![]() S△ABC;③ S四边形AEDF=ADEF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )
S△ABC;③ S四边形AEDF=ADEF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b、c满足![]() ,且a,b,c分别是点A,B,C在数轴上对应的数.
,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)求a,b,c的值,并在数轴上标出点A,B,C;
![]()
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
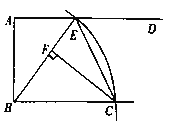
【题目】如图所示,AD∥BC,∠BAD=90°,以B为圆心,BC长为半径画弧,与射线AD相交于点E,连接BE,过C作CF⊥BE于点F.
(1)线段BF与图中哪条线段相等?写出来并加以证明;
(2)若AB=12,BC=13,P从E沿ED方向运动,Q从C出发向B运动,两点同时出发且速度均为每秒1个单位
①当 秒时,四边形EPCQ是矩形
②当 秒时,四边形EPCQ是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com