
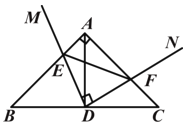
【题目】Rt△ ABC 中, AB=AC,点 D 为 BC 中点.∠ MDN=90°, ∠ MDN 绕点 D 旋转,DM、DN 分别与边 AB、AC 交于 E、F 两点.下列结论:① BE+CF=![]() BC;② S△AEF ≤
BC;② S△AEF ≤![]() S△ABC;③ S四边形AEDF=ADEF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )
S△ABC;③ S四边形AEDF=ADEF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】分析:先由ASA证明△AED≌△CFD,得出![]() ,再由勾股定理即可得出
,再由勾股定理即可得出![]() 从而判断①;设AB=AC=a,AE=CF=x,则AF=ax.先由三角形的面积公式得出
从而判断①;设AB=AC=a,AE=CF=x,则AF=ax.先由三角形的面积公式得出![]() 再根据二次函数的性质即可判断②;由勾股定理得到EF的表达式,利用二次函数性质求得EF最小值为
再根据二次函数的性质即可判断②;由勾股定理得到EF的表达式,利用二次函数性质求得EF最小值为![]() 而
而![]() 所以
所以![]() ,从而④错误;先得出
,从而④错误;先得出
S四边形AEDF=S△AED+S△ADF=S△CFD+S△ADF=S△ADC=![]() 再由
再由![]() 得到
得到![]()
∴ADEF>S四边形AEDF,所以③错误;如果四边形AEDF为平行四边形,则AD与EF互相平分,此时DF∥AB,DE∥AC,又D为BC中点,所以当E、F分别为AB、AC的中点时,AD与EF互相平分,从而判断⑤.
详解:∵Rt△ABC中,AB=AC,点D为BC中点,
∴![]() ,AD=BD=CD,
,AD=BD=CD,
∵![]()
∴![]()
∴∠ADE=∠CDF.
在△AED与△CFD中,
∵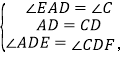
∴△AED≌△CFD(ASA),
∴AE=CF,
在Rt△ABD中,![]()
故①正确;
设AB=AC=a,AE=CF=x,则AF=ax.
∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值
有最大值![]()
又∵![]()
∴![]()
故②正确;
![]()
∴当![]() 时,
时,![]() 取得最小值
取得最小值![]()
∴![]() (等号当且仅当
(等号当且仅当![]() 时成立),
时成立),
而![]() ∴
∴![]()
故④错误;
由①的证明知△AED≌△CFD,
∴S四边形AEDF=S△AED+S△ADF=S△CFD+S△ADF=S△ADC=![]() ,
,
∵![]()
∴![]()
∴ADEF>S四边形AEDF,
故③错误;
当E.F分别为AB、AC的中点时,四边形AEDF为正方形,此时AD与EF互相平分.
故⑤正确。
综上所述,正确的有:①②⑤,共3个.
故选C.


科目:初中数学 来源: 题型:
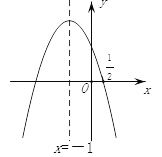
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点(![]() ,0),有下列结论:
,0),有下列结论:
①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0;⑤a-bm≥(am-b);其中所有正确的结论有( )个.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用粗线在数轴上表示了一个“范围”,这个“范围”包含所有大于1且小于2的数(数轴上1与2这两个数的点空心,表示这个范围不包含数1和2).

请你在数轴上表示出一个范围,使得这个范围:
(1)包含所有大于﹣3且小于0的数(画在数轴(1)上);
(2)包含﹣1.5、π这两个数,且只含有5个整数(画在数轴(2)上);
(3)同时满足以下三个条件:(画在数轴(3)上)
①至少有100对互为相反数和100对互为倒数;
②有最小的正整数;
③这个范围内最大的数与最小的数表示的点的距离大于3但小于4.
查看答案和解析>>
科目:初中数学 来源: 题型:
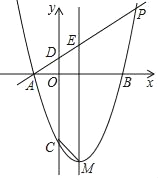
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=1,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.
(1)求点A的坐标和抛物线的表达式;
(2)当AE:EP=1:2时,求点E的坐标;
(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为20cm2,对角线交于点O,以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B…依此类推,则平行四边形AO2019C2020B的面积为( )cm2.

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中A(0,a)、B(b,0),且满足4(a﹣2)2+![]() (b﹣4)2=0,点P(m,m)在线段AB上
(b﹣4)2=0,点P(m,m)在线段AB上
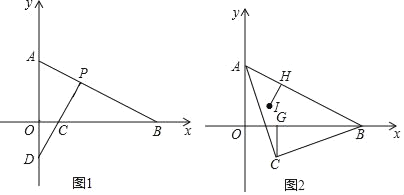
(1)求A、B的坐标;
(2)如图1,若过P作PC⊥AB交x轴于C,交y轴交于点D,求![]() 的值;
的值;
(3)如图2,以AB为斜边在AB下方作等腰直角△ABC,CG⊥OB于G,设I是∠OAB的角平分线与OP的交点,IH⊥AB于H.请探究![]() 的值是否发生改变,若不改变请求其值;若改变请说明理由.
的值是否发生改变,若不改变请求其值;若改变请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高科技创新意识,我市某中学在“2016年科技节”活动中举行科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛),各类别参赛人数统计如图:

请根据以上信息,解答下列问题:
(1)全体参赛的学生共有 人,“建模”在扇形统计图中的圆心角是 °;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类一等奖的学生为1名男生和1名女生,现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动,问选取的两人中恰为1男生1女生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的![]() 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.
(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
①-3,9,-27,81,-243,……
②-5,7,-29,79,-245,……
③- 1,3,-9,27,-81,……
(1)用乘方的方式表示第①行数中的第2 016个数;
(2)第②、第③行数与第①行数分别有什么关系?
(3)分别写出每行数的第10个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com