
【题目】在同一直角坐标系中,函数 ![]() 与y=ax+1(a≠0)的图象可能是( )
与y=ax+1(a≠0)的图象可能是( )
A.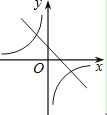
B.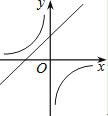
C.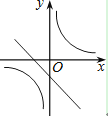
D.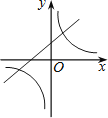
【答案】B
【解析】解答:∵a≠0, ∴a>0或a<0.
当a>0时,直线经过第一、二、三象限,双曲线经过第二、四象限,
当a<0时,直线经过第一、二、四象限,双曲线经过第一、三象限.
故选:B.
分析:因为a≠0,那么a>0或a<0.当a>0时,直线经过第一、二、三象限,双曲线经过第二、四象限,当a<0时,直线经过第一、二、四象限,双曲线经过第一、三象限,利用这些结论进行判断.直线y=kx+b、双曲线 ![]() ,当k>0时经过第一、三象限,当k<0时经过第二、四象限.
,当k>0时经过第一、三象限,当k<0时经过第二、四象限.
【考点精析】本题主要考查了反比例函数的图象的相关知识点,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D,F在x轴上,点C在DE边上,反比例函数y= ![]() (k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )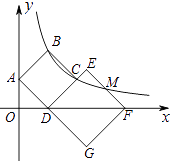
A.![]()
B.![]()
C.16
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.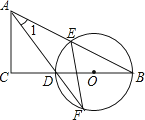
(1)求证:∠1=∠F.
(2)若sinB= ![]() ,EF=2
,EF=2 ![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1过点A(0,4),点D(4,0),直线l2:![]() 与x轴交于点C,两直线
与x轴交于点C,两直线![]() ,
,![]() 相交于点B.
相交于点B.
(1)求直线![]() 的解析式和点B的坐标;
的解析式和点B的坐标;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,正中设计一个圆形喷水池,若四周圆形和中间圆形的半径均为![]() 米,广场长为
米,广场长为![]() 米,宽为
米,宽为![]() 米.
米.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为500米,宽为300米,圆形花坛的半径为20米,求广场空地的面积(计算结果保留![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
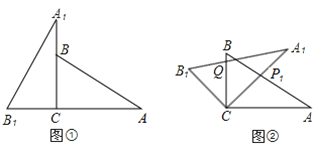
【题目】将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合,研究数轴我们发现:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为![]() .如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为
.如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为![]() =3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
=3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)用含t的代数式表示:t秒后,点P表示的数为 ,点Q表示的数为 .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数 ![]() (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,……以此类推,则a2018的值为( )
A. ﹣1007 B. ﹣1008 C. ﹣1009 D. ﹣2018
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com