
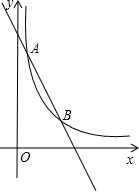
 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于点A(1,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于点A(1,6),B(3,n)两点.分析 (1)将A点坐标代入反比例函数解析式即可求出m的值,再将x=3代入反比例函数解析式解得n的值,由此得出B点的坐标,结合A、B两点的坐标,利用待定系数法即可求出一次函数的表达式;
(2)作点A关于y轴的对称点A′,连接A′B交y轴于点P,在y轴上任选一点不同于P点的P′点,由三角形内两边之和大于第三边来验证点P就是我们找到的使得PA+PB的值最小的点,由A点的坐标找出点A′的坐标,由待定系数法可求出直线A′B的函数表达式,令x=0即可得出P点的坐标;再结合三角形的面积公式与点到直线的距离即可求出△PAB的面积;
(3)设出点M的坐标,由MN⊥x轴,BD⊥y轴,可得出N、D的坐标,结合三角形的面积公式即可得出关于x的一元二次不等式,解不等式即可得出结论.
解答 解:(1)将点A(1,6)代入反比例函数y=$\frac{m}{x}$中,
得6=$\frac{m}{1}$,即m=6.
故反比例函数的解析式为y=$\frac{6}{x}$.
∵点B(3,n)在反比例函数y=$\frac{6}{x}$上,
∴n=$\frac{6}{3}$=2.
即点B的坐标为(3,2).
将点A(1,6)、点B(3,2)代入y=kx+b中,
得$\left\{\begin{array}{l}{6=k+b}\\{2=3k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-2}\\{b=8}\end{array}\right.$.
故一次函数的解析式为y=-2x+8.
(2)作点A关于y轴的对称点A′,连接A′B交y轴于点P,如图1所示.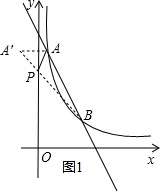
在y轴上任取一点P′(不同于点P),
∵A、A′关于y轴对称,
∴AP=A′P,AP′=A′P′,
在△P′A′B中,有A′P′+BP′=AP′+BP′>A′B=A′P+BP=AP+BP,
∴当A′、P、B三点共线时,PA+PB最小.
∵点A的坐标为(1,6),
∴点A′的坐标为(-1,6).
设直线A′B的解析式为y=ax+b,
将点A′(-1,6)、点B(3,2)代入到y=ax+b中,
得$\left\{\begin{array}{l}{6=-a+b}\\{2=3a+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-1}\\{b=5}\end{array}\right.$.
∴直线A′B的解析式为y=-x+5,
令x=0,则有y=5.
即点P的坐标为(0,5).
直线AB解析式为y=-2x+8,即2x+y-8=0.
AB=$\sqrt{(3-1)^{2}+(2-6)^{2}}$=2$\sqrt{5}$,点P到直线AB的距离d=$\frac{|5-8|}{\sqrt{{2}^{2}+{1}^{2}}}$=$\frac{3\sqrt{5}}{5}$.
△PAB的面积S=$\frac{1}{2}$AB•D=$\frac{1}{2}$×$\frac{3\sqrt{5}}{5}$×2$\sqrt{5}$=3.
(3)依照题意作出图形,如图2所示.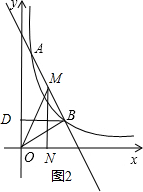
设M点的坐标为(x,-2x+8),则N点的坐标为(x,0).
∵点B为(3,2),
∴点D为(0,2).
∴OD=2,BD=3,ON=x,MN=8-2x.
∵△MON的面积大于△BOD的面积,
∴$\frac{1}{2}$ON•MN>$\frac{1}{2}$OD•BD,即x(8-2x)>2×3,
解得:1<x<3.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式、解一元二次不等式、点到直线的距离以及三角形的面积公式,解题的关键是:(1)算出B点的坐标;(2)找到P点的位置;(3)得出关于x的一元二次不等式.本题属于中档题,难度不大,解决该题型题目时,根据点在函数图象上求出点的坐标是关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:选择题
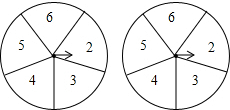 如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )| A. | $\frac{4}{25}$ | B. | $\frac{6}{25}$ | C. | $\frac{10}{25}$ | D. | $\frac{19}{25}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
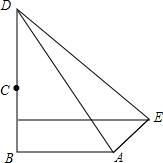 已知山顶上有一塔,山高BC为110米,小明在坡比为3:4的斜坡AE的底部A点测得塔顶D的仰角为45°,当他沿斜坡上行100米到达E时,测得塔顶D的仰角为19°,AB在同一水平线上,求塔高CD.(参考数据:tan19°≈0.35)
已知山顶上有一塔,山高BC为110米,小明在坡比为3:4的斜坡AE的底部A点测得塔顶D的仰角为45°,当他沿斜坡上行100米到达E时,测得塔顶D的仰角为19°,AB在同一水平线上,求塔高CD.(参考数据:tan19°≈0.35)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>-1 | B. | k>-1且k≠0 | C. | k≠0 | D. | k≥-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
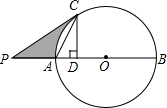 如图,已知⊙O的直径AB=10cm,C是⊙O上的一点,作CD⊥AB于点D,以C为顶点作∠PCA=∠ACD,交BA的延长线于点P,
如图,已知⊙O的直径AB=10cm,C是⊙O上的一点,作CD⊥AB于点D,以C为顶点作∠PCA=∠ACD,交BA的延长线于点P,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
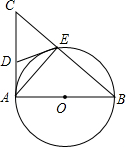 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E,连接AE.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com