
| A. | k>-1 | B. | k>-1且k≠0 | C. | k≠0 | D. | k≥-1 |
 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
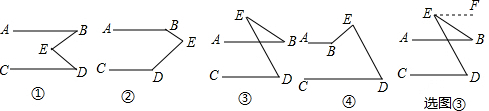
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
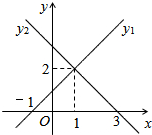 如图,已知一次函数y1=kx1+b1与一次函数y2=kx2+b2的图象相交于点(1,2),则不等式kx1+b1<kx2+b2的解集是x<1.
如图,已知一次函数y1=kx1+b1与一次函数y2=kx2+b2的图象相交于点(1,2),则不等式kx1+b1<kx2+b2的解集是x<1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
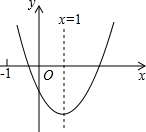 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:| A. | ①② | B. | ①④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
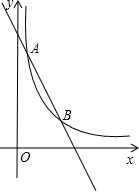 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于点A(1,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于点A(1,6),B(3,n)两点.查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )
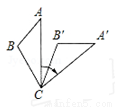
A. 30° B. 40° C. 80° D. 110°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com