
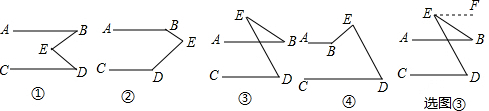
分析 (1)如图③,过点E作EF∥AB,根据两直线平行,内错角相等可得∠D=∠DEF,∠B=∠BEF,再根据∠BED=∠DEF-∠BEF整理即可得证;
(2)①过点E作EF∥AB,根据两直线平行,内错角相等解答;②过点E作EF∥AB,根据两直线平行,同旁内角互补解答;③延长AB与DE相交于点F,首先利用两直线平行,同位角相等,再利用外角的性质得出结论;
(3)如图4,过点E作EF∥AB,根据两直线平行,内错角相等可得∠D=∠DEF,∠B=∠BEF,再根据∠BED=∠BEF-∠DEF整理即可得证.
解答 解:(1)选图③.
过点E作EF∥AB
∵AB∥CD,
∴EF∥CD(平行于同一条直线的两直线平行),
∴∠D=∠DEF,∠B=∠BEF,
又∵∠BED=∠DEF-∠BEF,
∴∠BED=∠D-∠B.
故答案为:平行于同一条直线的两直线平行,∠DEF-∠BEF,∠D-∠B
(2)①,如图①,过点E作EF∥AB,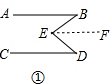
∵AB∥EF,AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠BEF,∠D=∠DEF,
∴∠BED=∠BEF+∠DEF=∠B+∠D;
②如图②,过点E作EF∥AB,
∵AB∥EF,AB∥CD,
∴AB∥EF∥CD,
∴∠B+∠BEF=180°,∠D+∠DEF=180°,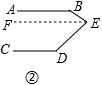
∴∠B+∠BEF+∠D+∠DEF=360°,
∴∠B+∠BED+∠D=360°,
∠BED=360°-∠B-∠D;
如图③延长AB与DE相交于点F,
∵AB∥CD,
∴∠EFB=∠D,
∵∠ABE=∠EFB+∠BED,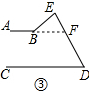
∴∠ABE=∠D+∠BED,
∠BED=∠ABE-∠D;
故答案为:∠B+∠D,∠BED=360°-∠B-∠D,∠ABE-∠D;
(3)选图4.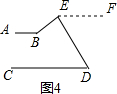
过点E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠D=∠DEF,∠B=∠BEF,
又∵∠BED=∠BEF-∠DEF,
∴∠BED=∠B-∠D.
点评 本题考查了平行线的性质,此类题目解题关键在于过拐点作平行线.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
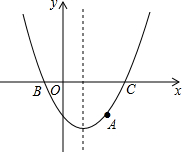 已知:二次函数的图象经过A(2,-3),对称轴x=1,抛物线与x轴两交点B、C的距离为4.
已知:二次函数的图象经过A(2,-3),对称轴x=1,抛物线与x轴两交点B、C的距离为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
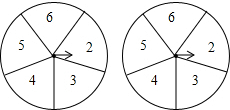 如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )| A. | $\frac{4}{25}$ | B. | $\frac{6}{25}$ | C. | $\frac{10}{25}$ | D. | $\frac{19}{25}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
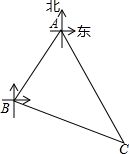 A,B,C三个城市的位置如图所示,城市B在城市A的西南方向(南偏西45°)100km处,城市C在城市A的南偏东30°方向,在城市B的南偏东75°方向.求城市A、C之间的距离.(结果取整数,参考数据:$\sqrt{6}$≈2.45)
A,B,C三个城市的位置如图所示,城市B在城市A的西南方向(南偏西45°)100km处,城市C在城市A的南偏东30°方向,在城市B的南偏东75°方向.求城市A、C之间的距离.(结果取整数,参考数据:$\sqrt{6}$≈2.45)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>-1 | B. | k>-1且k≠0 | C. | k≠0 | D. | k≥-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com