
【题目】如图,Rt△ABC中,∠C=90°,将△ABC沿AB向下翻折后,再绕点A按顺时针方向旋转α度(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB,BC于点G,H.
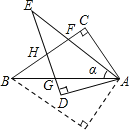
(1)判断∠CAF与∠DAG是否相等,并说明理由.
(2)求证:△ACF≌△ADG.
【答案】(1)∠CAF=∠DAG.理由见解析;(2)证明见解析.
【解析】
(1)由翻折和旋转的性质,可得∠BAC=∠EAD,同时减去∠BAE即可得结论;
(2)由翻折和旋转的性质,得到AC=AD,∠C=∠D,再加上(1)的结论,可判定全等.
(1)解:∠CAF=∠DAG.理由如下:
∵Rt△ABC中,∠C=90°,将△ABC沿AB向下翻折后,再绕点A按顺时针方向旋转α度(α<∠BAC),得到Rt△ADE,
∴∠BAC=∠EAD,
∵∠BAC=∠CAF+∠BAE,∠EAD=∠DAG+∠BAE,
∴∠CAF=∠DAG;
(2)证明:∵将△ABC沿AB向下翻折后,再绕点A按顺时针方向旋转α度(α<∠BAC),得到Rt△ADE,
∴AC=AD,∠C=∠D=90°,
在△ACF和△ADG中,
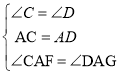 ,
,
∴△ACF≌△ADG(ASA).


科目:初中数学 来源: 题型:
【题目】为了解我市居民用水情况,在某小区随机抽查了20户家庭,并将这些家庭的月用水量进行统计,结果如下表:
月用水量(吨) | 4 | 5 | 6 | 8 | 13 |
户数 | 4 | 5 | 7 | 3 | 1 |
则关于这20户家庭的月用水量,下列说法正确的是( )
A.中位数是5B.平均数是5C.众数是6D.方差是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆 O 的半径为 1,过点 A(2,0)的直线与圆 O 相切于点 B,与 y 轴相交于点 C.
(1)求 AB 的长;
(2)求直线 AB 的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是角平分线,点E在AB上,且DE∥CA.
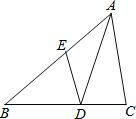
(1)△BDE与△BCA相似吗?为什么?
(2)已知AB=8,AC=6,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)求这个二次函数的表达式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c的对称轴l交x轴于点A.
(1)若此抛物线经过点(1,2),当点A的坐标为(2,0)时,求此抛物线的解析式;
(2)抛物线y=x2+bx+c交y轴于点B,将该抛物线平移,使其经过点A,B,且与x轴交于另一点C.若b2=2c,b≤﹣1,比较线段OB与OC+![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一元二次方程![]() 满足
满足![]() ,那么我们称这个方程为“凤凰”方程.已知
,那么我们称这个方程为“凤凰”方程.已知![]() 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC内接于⊙O,AC为⊙O的直径,点D为优弧BC的中点
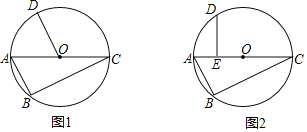
(1)如图1,连接OD,求证:AB∥OD;
(2)如图2,过点D作DE⊥AC,垂足为E.若AE=3,BC=8,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,![]() ).
).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com