练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．列方程或方程组解应用题：
    公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花（如图阴影部分），原空地一边减少了1m，另一边减少了2m，剩余空地的面积为20m2，求原正方形空地的边长．

    分析 可设原正方形的边长为xm，则剩余的空地长为（x-1）m，宽为（x-2）m．根据长方形的面积公式方程可列出，进而可求出原正方形的边长．

    解答 解：设原正方形空地的边长为xm，
    根据题意，得 （x-1）（x-2）=20，
    解方程，得 x1=6，x2=-3（舍），
    答：原正方形空地的边长为6m．

    点评 本题考查了一元二次方程的应用，应熟记长方形的面积公式．另外求得剩余的空地的长和宽是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

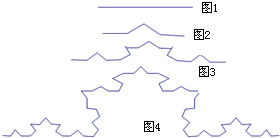    2．若图1中的线段长为1，将此线段三等分，并以中间的一段为边作等边三角形，然后去掉这一段，得到图2称第1次操作，再将图2中的每一段类似变形，得到图3即第2次操作，按上述方法继续得到图4为第3次操作，则第4次操作后折线的总长度为$\frac{64}{27}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．一元二次方程x2+x-1=0 的根的情况为（　　）
    A．有两个相等的实数根B．有两个不相等的实数根
    C．只有一个实数根D．没有实数根

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．某商场按定价销售某种商品时，每件商品可以获利30元，已知按定价的八五折销售该商品4件与将定价降低10元销售该商品3件所获得的利润相等，请求出该商品的进价和定价分别是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

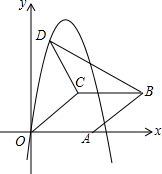    7．如图，在平面直角坐标系中，菱形OABC的顶点A在x轴正半轴上，顶点C的坐标为（4，3），D是抛物线y=-x2+6x上一点，且在x轴上方，则△BCD面积的最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

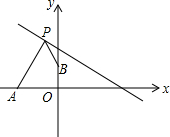    17．如图，点A的坐标为（-2，0），点B的坐标为（0，1），点P在直线y=-$\frac{1}{2}$x+2上运动，当线段|AP-BP|最长时，点P的坐标是（1，$\frac{3}{2}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．已知y与x-1成反比例，那么它的解析式为（　　）
    A．y=$\frac{k}{x}$-1（k≠0）B．y=k（x-1）（k≠0）C．y=$\frac{k}{x-1}$（k≠0）D．y=$\frac{x-1}{k}$（k≠0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．二次根式$\sqrt{x-\sqrt{2}}$中x的取值范围是（　　）
    A．x≥$\sqrt{2}$B．x≤$\sqrt{2}$C．x＜$\sqrt{2}$D．x＞$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

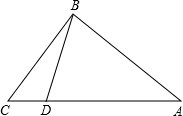    2．如图，在Rt△ABC中，∠ABC=90°，AB=20，BC=15，点D为AC边上的动点，点D从点C出发，沿边CA往A运动，当运动到点A时停止，设点D运动的时间为t秒，速度为每秒2个单位长度．
    （1）填空：当t=4.5或12.5秒时，△CBD是直角三角形；
    （2）若△CBD是等腰三角形，求t的值．

    查看答案和解析>>

    同步练习册答案