
【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:
⑴若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
⑵若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并求出最大获利。
甲 | 乙 | |
进价(元/件) | 15 | 35 |
售价(元/件) | 20 | 45 |
【答案】(1)甲100件,乙60件(2)1270元
【解析】分析: (1)设甲种商品应购进x件,乙种商品应购进y件,等量关系为:甲件数+乙件数=160,甲总利润+乙总利润=1100,(2)设出所需未知数,甲进价×甲数量+乙进价×乙数量<4300,甲总利润+乙总利润>1260.
(1)设甲种商品应购进x件,乙种商品应购进y件.
根据题意得:![]()
解得:![]()
答:甲种商品购进100件,乙种商品购进60件.
(2)设甲种商品购进a件,则乙种商品购进(160-a)件.
根据题意得![]()
解得:65<a<68.
∵a为非负整数,
∴a取66,67,
∴160-a相应取94,93,
方案一:甲种商品购进66件,乙种商品购进94件,获利1270元,
方案二:甲种商品购进67件,乙种商品购进93件,获利1265元,
答:有两种购货方案,其中获利最大的是1270元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AC=10,S△ABC =25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是( )

A. 4 B. ![]() C. 5 D. 6
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,以BC为边向外作△BCD并连接AD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,且点A,C,E在一条直线上,若AB=3,AC=2,求∠BAD的度数与AD的长?
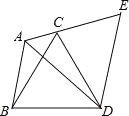
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②a﹣b+c<0;③2a+b﹣c<0;④4a+2b+c>0,⑤若点(﹣ ![]() ,y1)和(
,y1)和( ![]() ,y2)在该图象上,则y1>y2 . 其中正确的结论是(填入正确结论的序号)
,y2)在该图象上,则y1>y2 . 其中正确的结论是(填入正确结论的序号) 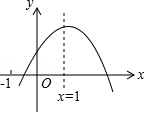
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国实施的“一带一路”战略方针,惠及沿途各国.中欧班列也已融入其中.从我国重庆开往德国的杜伊斯堡班列,全程约11025千米.同样的货物,若用轮船运输,水路路程是铁路路程的1.6倍,水路所用天数是铁路所用天数的3倍,列车平均日速(平均每日行驶的千米数)是轮船平均日速的2倍少49千米.分别求出列车及轮船的平均日速.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com