
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的一点,
上的一点,![]() ,点
,点![]() 从
从![]() 点出发沿射线
点出发沿射线![]() 方向以每秒
方向以每秒![]() 个单位的速度向右运动.设点
个单位的速度向右运动.设点![]() 的运动时间为
的运动时间为![]() .连结
.连结![]() .
.
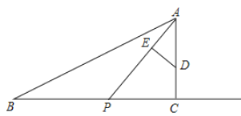
(1)当![]() 秒时,求
秒时,求![]() 的长度(结果保留根号);
的长度(结果保留根号);
(2)当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的值;
的值;
(3)过点![]() 做
做![]() 于点
于点![]() .在点
.在点![]() 的运动过程中,当
的运动过程中,当![]() 为何值时,能使
为何值时,能使![]() ?
?
【答案】(1)2![]() ;(2)4
;(2)4![]() 或16或5;(3)5或11.
或16或5;(3)5或11.
【解析】
(1)根据题意得BP=2t,从而求出PC的长,然后利用勾股定理即可求出AP的长;
(2)先利用勾股定理求出AB的长,然后根据等腰三角形腰的情况分类讨论,分别列出方程即可求出t的值;
(3)根据点P的位置分类讨论,分别画出对应的图形,根据勾股定理求出AE,分别利用角平分线的性质和判定求出AP,利用勾股定理列出方程,即可求出t的值.
(1)根据题意,得BP=2t,
∴PC=16-2t=16-2×3=10,
∵AC=8,
在Rt△APC中,根据勾股定理,得AP=![]() =
=![]() =2
=2![]() .
.
答:AP的长为2![]() .
.
(2)在Rt△ABC中,AC=8,BC=16,
根据勾股定理,得AB=![]() =
=![]() =8
=8![]()
若BA=BP,
则 2t=8![]() ,
,
解得:t=4![]() ;
;
若AB=AP,
∴此时AC垂直平分BP
则BP=32,
2t=32,
解得:t=16;
若PA=PB=2t,CP=16-2t
∵PA2= CP2+AC2
则(2t)2=(16-2t)2+82,
解得:t=5.
答:当△ABP为等腰三角形时,t的值为4![]() 、16、5.
、16、5.
(3)若P在C点的左侧,连接PD
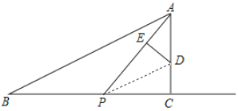
CP=16-2t
∵DE=DC=3,AC=8,![]() ,DC⊥PC
,DC⊥PC
∴PD平分∠EPC,AD=AC-DC=5
根据勾股定理可得AE=![]() ,
,
∴∠EPD=∠CPD
∴∠EDP=90°-∠EPD=90°-∠CPD=∠CDP
∴DP平分∠EDC
∴PE=CP=162t
∴AP=AE+EP=20-2t
∵PA2= CP2+AC2
则(20-2t)2=(16-2t)2+82,
解得:t=5;
若P在C点的右侧,连接PD
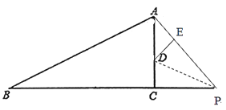
CP=2t-16
∵DE=DC=3,AC=8,![]() ,DC⊥PC
,DC⊥PC
∴PD平分∠EPC,AD=AC-DC=5
根据勾股定理可得AE=![]()
∴∠EPD=∠CPD
∴∠EDP=90°-∠EPD=90°-∠CPD=∠CDP
∴DP平分∠EDC
∴PE=CP=2t-16
∴AP=AE+EP=2t-12
∵PA2= CP2+AC2
则(2t-12)2=(2t-16)2+82,
解得:t=11;
答:当t为5或11时,能使DE=CD.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,E是□ABCD的边BC延长线上一点,AE交CD于点F,FG∥AD交AB于点G.
(1)填空:图中与△CEF相似的三角形有__________;(写出图中与△CEF相似的所有三角形)
(2)从(1)中选出一个三角形,并证明它与△CEF相似.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]()
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长为![]() ,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,李师傅想用长为80米的栅栏,再借助教学楼的外墙围成一个矩形的活动区![]() . 已知教学楼外墙长50米,设矩形
. 已知教学楼外墙长50米,设矩形![]() 的边
的边![]() 米,面积为
米,面积为![]() 平方米.
平方米.
(1)请写出活动区面积![]() 与
与![]() 之间的关系式,并指出
之间的关系式,并指出![]() 的取值范围;
的取值范围;
(2)当![]() 为多少米时,活动区的面积最大?最大面积是多少?
为多少米时,活动区的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明.
在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明.
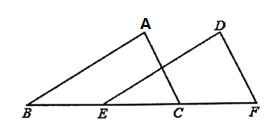
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
解:我写的真命题是:
在![]() 和
和![]() 中,已知:___________________.
中,已知:___________________.
求证:_______________.(不能只填序号)
证明如下:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方位角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在锐角三角形ABC中,AB=8,AC=5,BC=6,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,下列结论:①∠CBD=∠EBD,②DE⊥AB,③三角形ADE的周长是7,④![]() ,⑤
,⑤![]() .其中正确的个数有( )
.其中正确的个数有( )
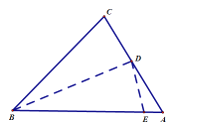
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.
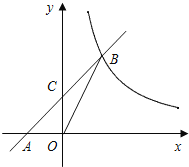
(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,点O是AC上一动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.
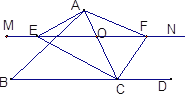
⑴说明:OE=OF
⑵当点O运动到何处时,四边形AECF是矩形,证明你的结论
⑶在⑵的条件下,当⊿ABC满足什么条件时,四边形AECF为正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com