
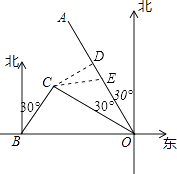
����Ŀ����ͼ��ʾ���ۿ�Bλ�ڸۿ�O��������120km����С��Cλ�ڸۿ�O��ƫ��60��ķ���һ���δ��Ӹۿ�O��������OA����ƫ��30�㣩��vkm/h���ٶ�ʻ��ۿ�O��ͬʱһ�ҿ�ͧ�Ӹۿ�B�������ر�ƫ��30��ķ�����60km/h���ٶ�ʻ��С��C����С��C��1h��װ�������ʺ�������ԭ�����ٶȸ��δ���ȥ��
��1����ͧ�Ӹۿ�B��С��C��Ҫ�ʱ�䣿
��2������ͧ��С��C�����δ�����ǡ����ʱ1h����v��ֵ����������ۿ�O�ľ��룮
���𰸡�
��1��
�⣺�ߡ�CBO=60�㣬��COB=30�㣬
���BCO=90�㣮
��Rt��BCO����OB=120��
��BC= ![]() OB=60��
OB=60��
���ͧ�Ӹۿ�B��С��C��ʱ��Ϊ��60��60=1��Сʱ��
��2��
�⣺��C��CD��OA������ΪD������ᴦΪ��E��
��OC=OBcos30��=60 ![]() ��CD=
��CD= ![]() OC=30
OC=30 ![]() ��OD=OCcos30��=90��
��OD=OCcos30��=90��
��DE=90��3v��
��CE=60��CD2+DE2=CE2��
�ࣨ30 ![]() ��2+��90��3v��2=602��
��2+��90��3v��2=602��
��v=20��40��
�൱v=20km/hʱ��OE=3��20=60km��
��v=40km/hʱ��OE=3��40=120km��
����������1��Ҫ��B��C��ʱ�䣬��֪���ٶȣ���ֻҪ���BC��·�̣�������·�̹�ʽ������������ʱ�䣻��2����C��CD��OA������ΪD������ᴦΪ��E�����OC=OBcos30��=60 ![]() ��CD=
��CD= ![]() OC=30
OC=30 ![]() ��OD=OCcos30��=90����DE=90��3v����ֱ�ǡ�CDE�����ù��ɶ����ó�CD2+DE2=CE2 �� ����30
��OD=OCcos30��=90����DE=90��3v����ֱ�ǡ�CDE�����ù��ɶ����ó�CD2+DE2=CE2 �� ����30 ![]() ��2+��90��3v��2=602 �� �ⷽ�����v=20��40�����������������ۿ�O�ľ��룮
��2+��90��3v��2=602 �� �ⷽ�����v=20��40�����������������ۿ�O�ľ��룮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊ������Ȥζ�˶�����ȡ�úóɼ���Ա�����ƻ�����ס������ֽ�Ʒ��20�������м��ֽ�Ʒÿ��40Ԫ�����ֽ�Ʒÿ��30Ԫ��
��1���������ס������ֽ�Ʒ��������650Ԫ����ס������ֽ�Ʒ�������˶��ټ���
��2������������ֽ�Ʒ�ļ������������ֽ�Ʒ������2�����ܻ��Ѳ�����680Ԫ����ù�˾���ļ�����ͬ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�Բֱ�����뾶OC��AB�ڵ�O��ADƽ�֡�CAB���� ![]() �ڵ�D������CD��OD�����н��ۣ���AC��OD����CE=OE���ۡ�OED=��AOD����CD=DE��������ȷ���۵ĸ����У� ��
�ڵ�D������CD��OD�����н��ۣ���AC��OD����CE=OE���ۡ�OED=��AOD����CD=DE��������ȷ���۵ĸ����У� �� 
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������a��b��c�������ϵ�λ����ͼ��ʾ����|a|=|b|��
��1��a+b=�� ����![]() =�� ����
=�� ����
��2���ж�b+c��a��c����b+c����a��b���ķ��ţ�
��3���ж�![]() �ķ��ţ�
�ķ��ţ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B�����������ϵ�λ����ͼ��ʾ������OΪԭ�㣬��A��Ӧ��������Ϊ��4����B��Ӧ��������Ϊ6��
��1������P�ӵ�A��������ÿ��2����λ���ȵ��ٶ������˶������˶�ʱ��Ϊt�루t��0����
�ٵ�t=1ʱ��AP�ij�Ϊ�� ������P��ʾ��������Ϊ�� ����
�ڵ�PB=2ʱ����t��ֵ��
��2���������P��ÿ��6����λ���ȵ��ٶȴ�O�������˶�����A��B�ֱ���ÿ��1����λ���Ⱥ�ÿ��3����λ���ȵ��ٶ������˶���������ͬʱ��������ô��������PA=2PB��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��������Ʒ�г�ָ����Ϊÿǧ��150Ԫ����˾��ʵ�����ۼ۸���Ը���x���ٷֵ㣨�����ۼ۸�=150��1+x%�����������г����з��֣�������Ʒ����������p��ǧ�ˣ������ۼ۸��İٷֵ�x֮��ĺ�����ϵΪp=��2x+24�����ù�˾��������12���ٷֵ�ļ۸���ۣ�ÿ����Ʒ�Կɻ���10%��
��1����ù�˾��������ÿǧ����Ʒ�ijɱ�Ϊ����Ԫ��
��2�����ù�˾����Ʒ����Ϊ����Ԫʱ������������Ϊ576Ԫ����˵��������������=�����ۼ۸�һ�ɱ���������������
��3���ù�˾����ÿ����һǧ����Ʒ�;���aԪ����a��1����ϣ�����̣���˾ͨ�����ۼ�¼���֣����۸��İٷֵ���ک�1ʱ���۳��������������������x���������С��ֱ��д��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������һ������x�ˣ��ڶ�����ȵ�һ����������![]() ��20�ˣ�����ӵڶ��������15�˵���һ���䣬��ô
��20�ˣ�����ӵڶ��������15�˵���һ���䣬��ô
��1��������һ���������Ϊ�� ���ˣ��ڶ����������Ϊ�� ���ˣ�
��2��������һ����������ȵڶ����������������ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD-A1B1C1D1���ⳤΪ1���ڡ��������dz�ͬʱ�ӵ�A����������ͬ���ٶȷֱ�������ǰ���У��ڼdz����е�·����AA1��A1D1�������dz����е�·����AB��BB1���������Ҷ���ѭ���¹��������еĵ�n+2���n�������ڵ�ֱ�߱���Ȳ�ƽ��Ҳ���ཻ������n��������������ô���ڡ��������dz���������2017����ֱ�ֹͣ�������������嶥�㴦ʱ������֮��ľ������� ��

A. 0 B. 1 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P1��һ��뾶Ϊ1�İ�Բ��ֽ�壬��P1�����϶˼�ȥһ��ֱ��Ϊ1�İ�Բ��õ�ͼ��P2��Ȼ�����μ�ȥһ����С�İ�Բ(��ֱ��Ϊǰһ������ȥ�İ�Բ�İ뾶)�õ�ͼ��P3��P4��Pn��,��ֽ��Pn�����ΪSn����S2018-S2019��ֵΪ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com