
【题目】阅读理解题
阅读材料:
两个两位数相乘,如果这两个因数的十位数字相同,个位数字的和是10,该类乘法的速算方法是:将一个因数的十位数字与另一个因数的十位数字加1的和相乘,所得的积作为计算结果的前两位,将两个因数的个位数字之积作为计算结果的后两位(数位不足两位,用0补齐)。
比如![]() ,它们乘积的前两位是
,它们乘积的前两位是![]() ,它们乘积的后两位是
,它们乘积的后两位是![]() ,所以
,所以![]() ;
;
再如![]() ,它们乘积的前两位是
,它们乘积的前两位是![]() ,它们乘积的后两位是
,它们乘积的后两位是![]() ,所以
,所以![]() ;
;
又如![]() ,
,![]() ,不足两位,就将6写在百位:
,不足两位,就将6写在百位:![]() ,不足两位,就将9写在个位,十位上写0,所以
,不足两位,就将9写在个位,十位上写0,所以![]()
该速算方法可以用我们所学的整式乘法与分解因式的知识说明其合理性;
设其中一个因数的十位数字为![]() ,个位数字是
,个位数字是![]() ,(
,(![]() 、
、![]() 表示1~9的整数),则该数可表示为
表示1~9的整数),则该数可表示为![]() ,另一因数可表示为
,另一因数可表示为![]() .
.
两数相乘可得:
![]()
![]()
![]()
![]()
![]() .
.
(注:其中![]() 表示计算结果的前两位,
表示计算结果的前两位,![]() 表示计算结果的后两位。)
表示计算结果的后两位。)
问题:
两个两位数相乘,如果其中一个因数的十位数字与个位数字相同,另一因数的十位数字与个位数字之和是10.
如![]() 、
、![]() 、
、![]() 等.
等.
(1)探索该类乘法的速算方法,请以![]() 为例写出你的计算步骤;
为例写出你的计算步骤;
(2)设十位数字与个位数字相同的因数的十位数字是![]() ,则该数可以表示为___________.
,则该数可以表示为___________.
设另一个因数的十位数字是![]() ,则该数可以表示为___________.(
,则该数可以表示为___________.(![]() 、
、![]() 表示1~9的正整数)
表示1~9的正整数)
(3)请针对问题(1)(2)中的计算,模仿阅读材料中所用的方法写出如:![]() 的运算式:____________________
的运算式:____________________
【答案】(1)4×(7+1)=32,4×3=12,44×73=3212;(2)11a,9b+10;(3)( 10a+a) ( 10b+c)= ( b+1 ) a×100+ac.
【解析】
(1)设一个因数的两个数字为b和c且b+c=10,另一个因数个位数为a,则另一个因数为10a+a,则 可得出( 10a+a) ( 10b+c)= ( b+1 ) a×100+ac.
规律:先将和为10的数的十位数字加1 ,再与后一个乘数的十位数字相乘后乘以100,然后加上两个个位数之积,由此可得出结论;
(2)根据两位数的表示方法即可得出结论.
(3)根据(1)即可得出结论.
(1)设一个因数的两个数字为b和c且b+c=10,另一个因数个位数为a,则另一个因数为10a+a,则( 10a+a) ( 10b+c)=100ab+10ac+10ab+ac=100ab+10(b+c)a+ac=100ab+10×10a+ac=( b+1 ) a×100+ac.
规律:先将和为10的数的十位数字加1 ,再与后一个乘数的十位数字相乘后乘以100,然后加上两个个位数之积,∴4×(7+1)=32,4×3=12,44×73=3212;
(2)设十位数字与个位数字相同的因数的十位数字是a,则该数可以表示为10a+a=11a.
设另一个因数的十位数字是b,则该数可以表示为10b+(10-b)=9b+10.
故答案为:11a,9b+10.
(3)设一个因数的两个数字为b和c且b+c=10,另一个因数个位数为a,则另一个因数为10a+a,则( 10a+a) ( 10b+c)=100ab+10ac+10ab+ac=100ab+10(b+c)a+ac=100ab+10×10a+ac=( b+1 ) a×100+ac.
故答案为:( 10a+a) ( 10b+c)= ( b+1 ) a×100+ac.


科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(6,4)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )

A. (2,12)
B. (﹣2,0)
C. (2,12)或(﹣2,0)
D. (12,2)或(﹣2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=4![]() ,CQ=10,则正方形ABCD的面积为 .
,CQ=10,则正方形ABCD的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
(1)求一次函数y=kx+b的关系式;
(2)结合图象,直接写出满足kx+b>![]()
![]() 的x的取值范围;
的x的取值范围;
(3)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分7分)已知关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使此方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
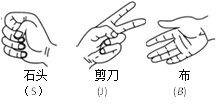
【题目】小明和小亮两人玩“石头、剪刀、布”的游戏,游戏规则为:石头胜剪刀,剪刀胜布,布胜石头,相同则不分胜负.
(1)请用列表法或画树状图表示出所有可能出现的游戏结果;
(2)求小明获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
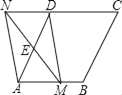
【题目】如图,在菱形ABCD中,AB=4,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)当AM的值为 时,四边形AMDN是矩形,请你把猜想出的AM值作为已知条件,说明四边形AMDN是矩形的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为2:3,甲、乙两车离AB中点C路程y(千米)与甲车出发时间t(小时)的关系图象如图所示,则下列说法:①A、B两地之间的距离为180千米;②乙车的速度为36千米/小时;③a=3.75;④当乙车到达终点时,甲车距离终点还有30千米.其中正确的结论有( )
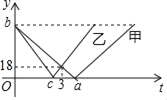
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的面积为32,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )

A. 8 B. 6 C. 4 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com