
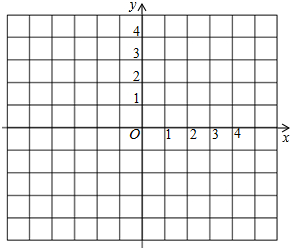
 如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).
如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).分析 (1)利用平面坐标系画出图形,然后根据△ABC的面积=S正方形ECFM-S△ECA-S△NAB-S△BCF求出即可;
(2)根据题意求得PB,即可求得P的坐标.
解答 解:(1)在平面直角坐标系中画出△ABC如图所示:
${S_{△ABC}}={S_{梯形OACD}}-{S_{△OAB}}-{S_{△BCD}}=\frac{1}{2}(1+3)×4-\frac{1}{2}×1×2-\frac{1}{2}×2×3$=8-1-3=4;
(2)由题意可知△ABP的面积=$\frac{1}{2}$×PB×OA=4,
∵OA=1,
∴PB=8,
∴P(-6,0)或(10,0).
点评 此题考查了坐标和图形的关系以及三角形的面积,找到各点的对应点,是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
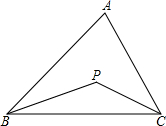 如图所示,BP、CP分别为∠ABC,∠ACB的角平分线,两线交于点P.
如图所示,BP、CP分别为∠ABC,∠ACB的角平分线,两线交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
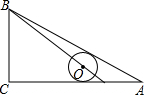 在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )
在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )| A. | 2-$\sqrt{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{3}}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解北京市中学生的视力情况 | |
| B. | 调查某品牌食品的色素含量是否符合国家标准 | |
| C. | 了解全班同学参加社会实践活动时间 | |
| D. | 调查春节联欢晚会的收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
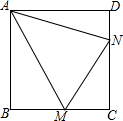 已知正方形ABCD中,∠MAN=45°,且∠MAN的两边分别交BC、DC于点M、N.试猜想线段BM、DN和MN之间的数量关系,写出猜想,并加以证明.
已知正方形ABCD中,∠MAN=45°,且∠MAN的两边分别交BC、DC于点M、N.试猜想线段BM、DN和MN之间的数量关系,写出猜想,并加以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com