
【题目】如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF
(1)求证:△ACD≌△CBF
(2)以AD为边作等边三角形△ADE,点D在线段BC上的何处时,四边形CDEF是平行四边行.
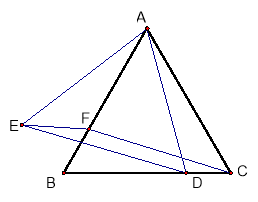
【答案】(1)证明过程见解析;(2)中点
【解析】
试题分析:(1)首先根据等边三角形的性质得出AC=BC,∠ACD=∠B=60°,结合CD=BF得出三角形全等;(2)根据D为中点得出F为中点,根据等边三角形的性质得出AD⊥BC,CF⊥AB,∠FCB=∠BAD=30°,根据△ADE也是等边三角形得出∠BDE=30°,则DE∥CF,结合CF=AD=DE得出平行四边形.
试题解析:(1)∵△ABC为等边三角形 ∴AC=BC,∠ACD=∠B=60° 又∵CD=BF
∴△ACD≌△CBF
(2)D在BC的中点时,四边形CDFE是平行四边形
∵D是BC中点 ∴F是 AB中点 ∴AD⊥BC,CF⊥AB ∴∠FCB=30°,∠BAD=30°
又△ADE也是等边三角形 ∴∠BDE=30° ∴DE∥CF 又CF=AD=DE ∴四边形是CDEF平行四边形


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】将抛物线 C1:y=a(x-h)2+k先向右平移4个单位,再向上平移1个单位得到抛物线C2:y=-7x2,
则抛物线C1的解析式为__________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
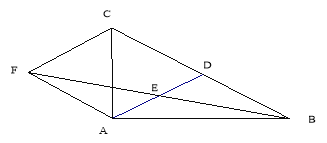
【题目】 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com