
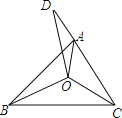
【题目】如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=92°,则∠BCA的度数为 .
【答案】42°.
【解析】
试题分析:可证明△COD≌△COB,根据全等三角形的性质得到∠D=∠CBO,再根据邻补角的定义得到∠BAD=88°,由角平分线的定义得到∠BAO=46°,从而得出∠DAO=134°,根据等腰三角形的性质得到∠D=23°,即可得出∠CBO=23°,然后根据三角形的内角和即可得到结论.
解:∵△ABC三个内角的平分线交于点O,
∴∠ACO=∠BCO,
在△COD和△COB中,
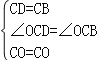 ,
,
∴△COD≌△COB,
∴∠D=∠CBO,
∵∠BAC=92°,
∴∠BAD=88°,
∴∠BAO=46°,
∴∠DAO=134°,
∵AD=AO,∴∠D=23°,
∴∠CBO=23°,
∴∠ABC=46°,
∴∠BCA=42°,
故答案为:42°.



科目:初中数学 来源: 题型:
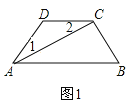
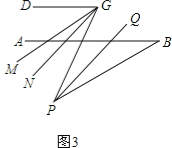
【题目】 (1)、如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明;
(2)如图,在(1)的条件下,AB的下方两点E,F满足:BF平分∠ABE,CF 平分∠DCE,若∠CFB=20°,∠DCE=70°,求∠ABE的度数
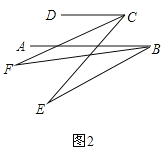
(3)在前面的条件下,若P是BE上一点;G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP﹣∠MGN的值不变;②∠MGN 的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.
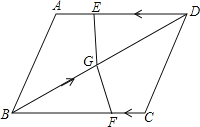
(1)试说明:AD∥BC;
(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能化简(x-1)(x99+x98+x97+……+x+1)吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.
分别计算下列各式的值:
①(x-1)(x+1)=x2-1;
②(x-1)(x2+x+1)=x3-1;;
③(x-1)(x3+x2+1)=x4-1;;……
由此我们可以得到:(x-1)(x99+x98+x97+…+x+1)=________________;
请你利用上面的结论,完成下面两题的计算,并写出计算过程:
(1) 299+298+297+……+2+1;
(2)(-2)50+(-2)49+(-2)48+……+(-2)+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,求抛物线经过A(1,0),C(0,3)两点,与x轴交于A、B两点.
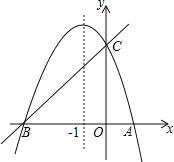
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在该抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为该抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.(提示:若平面直角坐标系内两点P(x1,y1)、Q(x2,y2),则线段PQ的长度PQ=![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(﹣3,0),∠B=30°,则点B的坐标为( )
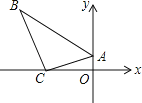
A.(﹣3﹣![]() ,3)
,3)
B.(﹣3﹣![]() ,3
,3![]() )
)
C.(﹣![]() ,3)
,3)
D.(﹣![]() ,3
,3![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com