
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=��1���������߾���A��1��0����C��0��3�����㣬��x�ύ��A��B���㣮
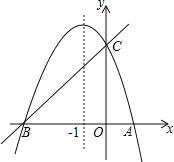
��1����ֱ��y=mx+n����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
��2���ڸ������ߵĶԳ���x=��1����һ��M��ʹ��M����A�ľ����뵽��C�ľ���֮����С�������M�����ꣻ
��3�����PΪ�������ߵĶԳ���x=��1�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮����ʾ����ƽ��ֱ������ϵ������P��x1��y1����Q��x2��y2�������߶�PQ�ij���PQ=![]() ����
����
���𰸡���1��ֱ���Ľ���ʽ��y=x+3�������ߵĽ���ʽ��y=��x2��2x+3����2��M�������ǣ���1��2������3��P�������ǣ���1����1����1��2����1��4����1����2����
��������
�����������1������A��B����x=��1�ԳƼ������B�����꣬Ȼ�����ô���ϵ����������������ߵĽ���ʽ��
��2�����BC��Գ���Ľ������M��
��3����P�������ǣ���1��p������������֮��ľ��빫ʽ��ʾ��BC��BP��PC�ij���Ȼ��ֳ���BPC�����߷ֱ���б������������ۣ����ù��ɶ����з������p��ֵ���õ�P�����꣮
�⣺��1��A��1��0������x=��1�ĶԳƵ��ǣ���3��0������B�������ǣ���3��0����
��������ã�![]() ��
��
��ã�![]() ��
��
�������ߵĽ���ʽ��y=x+3��
��������ã�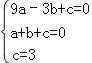 ��
��
��ã�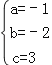 ��
��
�������ߵĽ���ʽ��y=��x2��2x+3��
��2����y=x+3����x=��1����y=��1+3=2��
��M�������ǣ���1��2����
��3����P�������ǣ���1��p����
��BP2=����1+3��2+p2=4+p2��
PC=��0+1��2+��3��p��2=p2��6p+10��
BC=32+32=18��
��BCʱб��ʱ��BP2+PC2=BC2����4+p2��+��p2��6p+10��=18��
��ã�p=��1��2��
��P�������ǣ���1����1����1��2����
��BP��б��ʱ��BP2=PC2+BC2����4+p2=��p2��6p+10��+18��
��ã�p=4��
��P�������ǣ���1��4����
��PC��б��ʱ��PC2=BP2+BC2����p2��6p+10=4+p2+18��
��ã�p=��2��
��P�������ǣ���1����2����
��֮��P�������ǣ���1����1����1��2����1��4����1����2����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ξ�ͳ�ƣ����ꡰ�塤һ��С�����ڼ䣬���и����ξ�����Ʊ����Լ2300��Ԫ�����ݡ�2300���ÿ�ѧ��������ʾΪ______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������ε��ڽǺ���������Ǻ͵�4�������������ǣ� ������.
A. 6 B. 9 C. 8 D. 10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
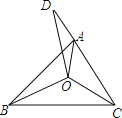
����Ŀ����ͼ����֪��ABC�����ڽǵ�ƽ���߽��ڵ�O����D��CA���ӳ����ϣ���DC=BC��AD=AO������BAC=92��������BCA�Ķ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����������ȷֱ�Ϊ4cm��9cm��ľ�������붤һ��������ľ�������������г��ȵļ���ľ������Ӧ��ѡ���ľ���ij���ֻ����( )
A. 5cm B. 3cm C. 17cm D. 12cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ����( )
A. ���ཻ�������߶���ƽ���� B. ���ཻ������ֱ����ƽ����
C. ���ཻ������������ƽ���� D. ��ͬһƽ����,���ཻ������ֱ����ƽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����װ������ij���װ��һ����װ�ı��Ϊ300Ԫ��������۵İ������ۣ��Կɻ���50%��������װÿ���Ľ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺
��������
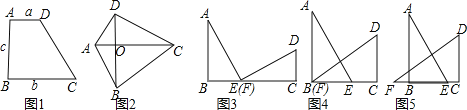
���Ƕ�֪������ͼ1�����ı���ABCD�У�AD��BC����B=90������AD=a��BC=b��AB=c����ô�ı���ABCD�����S=![]() ��
��
��ͼ2�����ı���ABCD�У������Խ���AC��BD������ΪO�����ı���ABCD�����=![]() AC��OD+
AC��OD+![]() AC��OB=
AC��OB=![]() AC����OD+OB��=
AC����OD+OB��=![]() AC��BD��
AC��BD��
������⣺
��1��������a��b Ϊֱ�DZߣ�cΪб��������ȫ�ȵ�ֱ����ABE����FCD����ƴ����ͼ3��ʾ��ͼ�Σ�ʹB��E��F��C�ĵ���һ��ֱ���ϣ���ʱE��F�غϣ�����֪��ABE�ա�FCD��AE��DF�� ����֤����a2+b2=c2��
��2���̶���FCD���ٽ���ABE����BCƽ�Ƶ���ͼ4��ʾ��λ�ã���ʱB��F�غϣ����������֤����a2+b2=c2��
��3������ABEƽ�Ƶ���ͼ5��λ�ã�����a2+b2=c2�������������������д��֤�����̣��������������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com