
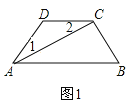
【题目】 (1)、如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明;
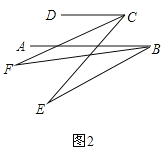
(2)如图,在(1)的条件下,AB的下方两点E,F满足:BF平分∠ABE,CF 平分∠DCE,若∠CFB=20°,∠DCE=70°,求∠ABE的度数
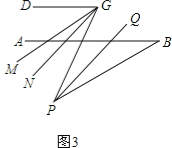
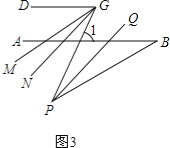
(3)在前面的条件下,若P是BE上一点;G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP﹣∠MGN的值不变;②∠MGN 的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值.
【答案】(1)、AB∥CD;理由见解析;(2)、30°;(3)、①∠DGP﹣∠MGN的值随∠DGP的变化而变化;②∠MGN的度数为15°不变;证明过程见解析.
【解析】
试题分析:(1)、根据角平分线得出∠1=∠CAB,从而得出∠2=∠CAB,从而说明平行线;(2)、根据角平分线的性质得出∠DCF=![]() ∠DCE=35°,∠ABE=2∠ABF,根据CD∥AB得出∠2=∠DCF=35°,根据∠2=∠CFB+∠ABF,∠CFB=20°得出∠ABF和∠ABE的度数;(3)、根据三角形外角性质得出∠1=∠BPG+∠B,根据角平分线的性质得出∠GPQ=
∠DCE=35°,∠ABE=2∠ABF,根据CD∥AB得出∠2=∠DCF=35°,根据∠2=∠CFB+∠ABF,∠CFB=20°得出∠ABF和∠ABE的度数;(3)、根据三角形外角性质得出∠1=∠BPG+∠B,根据角平分线的性质得出∠GPQ=![]() ∠BPG,∠MGP=
∠BPG,∠MGP=![]() ∠DGP,根据AB∥CD得出∠MGP=
∠DGP,根据AB∥CD得出∠MGP=![]() (∠BPG+∠B),根据PQ∥GN得出∠NGP=∠GPQ=
(∠BPG+∠B),根据PQ∥GN得出∠NGP=∠GPQ=![]() ∠BPG,从而根据∠MGN=∠MGP﹣∠NGP=
∠BPG,从而根据∠MGN=∠MGP﹣∠NGP=![]() ∠B,从而得出答案.
∠B,从而得出答案.
试题解析:(1)、AB∥CD.
∵AC平分∠DAB, ∴∠1=∠CAB, ∵∠1=∠2, ∴∠2=∠CAB, ∴AB∥CD;
(2)、如图2, ∵BF平分∠ABE,CF平分∠CDE, ∴∠DCF=![]() ∠DCE=35°,∠ABE=2∠ABF, ∵CD∥AB,
∠DCE=35°,∠ABE=2∠ABF, ∵CD∥AB,
∴∠2=∠DCF=35°, ∵∠2=∠CFB+∠ABF,∠CFB=20°, ∴∠ABF=15°, ∴∠ABE=2∠ABF=30°
(3)、如图3,根据三角形的外角性质,∠1=∠BPG+∠B, ∵PQ平分∠BPG,GM平分∠DGP,
∴∠GPQ=![]() ∠BPG,∠MGP=
∠BPG,∠MGP=![]() ∠DGP, ∵AB∥CD, ∴∠1=∠DGP, ∴∠MGP=
∠DGP, ∵AB∥CD, ∴∠1=∠DGP, ∴∠MGP=![]() (∠BPG+∠B),
(∠BPG+∠B),
∵PQ∥GN, ∴∠NGP=∠GPQ=![]() ∠BPG, ∴∠MGN=∠MGP﹣∠NGP=
∠BPG, ∴∠MGN=∠MGP﹣∠NGP=![]() (∠BPG+∠B)﹣
(∠BPG+∠B)﹣![]() ∠BPG=
∠BPG=![]() ∠B,
∠B,
根据前面的条件,∠B=30°, ∴∠MGN=![]() ×30°=15°,
×30°=15°,
∴①∠DGP﹣∠MGN的值随∠DGP的变化而变化;②∠MGN的度数为15°不变.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
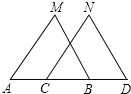
A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2012m停下,则这个微型机器人停在( )

A.点A处 B.点B处 C.点C处 D.点E处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一元二次方程x2﹣2x﹣a=0无实数根,则一次函数y=(a+1)x+(a﹣1)不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据威海市旅游局统计,今年“五·一”小长假期间,我市各旅游景点门票收入约2300万元,数据“2300万”用科学记数法表示为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简(幂的运算)
(1).m3·m·(m2)3 (2).(p![]() q)4÷(q
q)4÷(q![]() p)3·(p
p)3·(p![]() q)2.
q)2.
(3).(![]() 3a3)3
3a3)3![]() a5·(
a5·(![]() 3a2)2 (4).22
3a2)2 (4).22![]() (
(![]() 2)-2
2)-2 ![]() 32÷(3.14
32÷(3.14![]()
![]() )0.
)0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com