
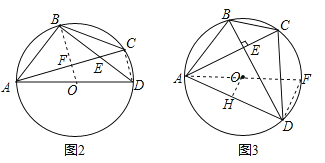
【题目】已知:⊙O上两个定点A,B和两个动点C,D,AC与BD交于点E.
(1)如图1,求证:EAEC=EBED;
(2)如图2,若![]() ,AD是⊙O的直径,求证:ADAC=2BDBC;
,AD是⊙O的直径,求证:ADAC=2BDBC;
(3)如图3,若AC⊥BD,点O到AD的距离为2,求BC的长.

【答案】(1)证明见试题解析;(2)证明见试题解析;(3)4.
【解析】
试题分析:(1)由同弧所对的圆周角相等得到角相等,从而证得三角形相似,于是得到结论;
(2)如图2,连接CD,OB交AC于点F由B是弧AC的中点得到∠BAC=∠ADB=∠ACB,且AF=CF=0.5AC.证得△CBF∽△ABD.即可得到结论;
(3)如图3,连接AO并延长交⊙O于F,连接DF得到AF为⊙O的直径于是得到∠ADF=90°,过O作OH⊥AD于H,由三角形的中位线定理得到DF=2OH=4,通过△ABE∽△ADF,得到1=∠2,于是结论可得.
试题解析:(1)∵∠EAD=∠EBC,∠BCE=∠ADE,∴△AED∽△BEC,∴![]() ,∴EAEC=EBED;
,∴EAEC=EBED;
(2)如图2,连接CD,OB交AC于点F,∵B是弧AC的中点,∴∠BAC=∠ADB=∠ACB,且AF=CF=0.5AC.又∵AD为⊙O直径,∴∠ABC=90°,又∠CFB=90°,∴△CBF∽△ABD.∴![]() ,故CFAD=BDBC,∴ACAD=2BDBC;
,故CFAD=BDBC,∴ACAD=2BDBC;
(3)如图3,连接AO并延长交⊙O于F,连接DF,∴AF为⊙O的直径,∴∠ADF=90°,过O作OH⊥AD于H,∴AH=DH,OH∥DF,∵AO=OF,∴DF=2OH=4,∵AC⊥BD,∴∠AEB=∠ADF=90°,∵∠ABD=∠F,∴△ABE∽△ADF,∴∠1=∠2,∴![]() ,∴BC=DF=4.
,∴BC=DF=4.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】若a、b、c是同一平面内三条不重合的直线,则它们的交点可以有( )
A. 1个或2个或3个 B. 0个或1个或2个或3个
C. 1个或2个 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABD和等边三角形CBD的边长均为a,现把它们拼合起来,E是AD上异于A、D两点的一动点,F是CD上一动点,满足AE+CF=a.则△BEF的形状如何?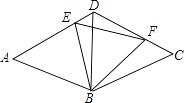
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1(注:与图2完全相同),二次函数![]() 的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现)
在计算器上输入一个正数,不断地按“![]() ”键求算术平方根,运算结果越来越接近1或都等于1.
”键求算术平方根,运算结果越来越接近1或都等于1.
【提出问题】
输入一个实数,不断地进行“乘以常数k,再加上常数b”的运算,有什么规律?
【分析问题】
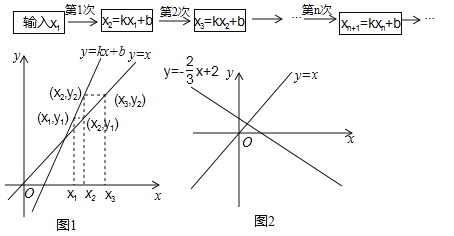
我们可用框图表示这种运算过程(如图a).
也可用图象描述:如图1,在x轴上表示出x1,先在直线y=kx+b上确定点(x1,y1),再在直线y=x上确定纵坐标为y1的点(x2,y1),然后再x轴上确定对应的数x2,…,以此类推.
【解决问题】
研究输入实数x1时,随着运算次数n的不断增加,运算结果x,怎样变化.
(1)若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;
(2)若k>1,又得到什么结论?请说明理由;
(3)①若![]() ,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2,x3,x4,并写出研究结论;
,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2,x3,x4,并写出研究结论;
②若输入实数x1时,运算结果xn互不相等,且越来越接近常数m,直接写出k的取值范围及m的值(用含k,b的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com