
【题目】(本小题满分8分)
阅读材料:
如图,在四边形ABCD中,对角线AC⊥BD,垂足为P.
求证:S四边形ABCD=![]()
证明:AC⊥BD→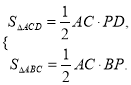
∴S四边形ABCD=S△ACD+S△ACB= ![]()
=![]()
解答问题:
(1)上述证明得到的性质可叙述为_______________________________________.
(2)已知:如图,等腰梯形ABCD中,AD∥BC,对角线AC⊥BD且相交于点P,AD=3cm,BC=7cm,利用上述的性质求梯形的面积.
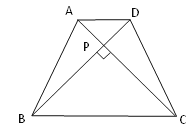
【答案】(1)对角线互相垂直的四边形的面积等于对角线乘积的一半. (2)S梯形=25(cm2).
【解析】试题分析:本题的关键是求出AC,BD的长,可过A,D分别作BC的垂线AE,DF,在直角三角形BFD中,可根据两底的差求出BE,CF的长,也就求出了BF,CE的长,要求BD还需知道直角三角形中一个锐角的度数,可通过全等三角形ACB和DBC得出∠DBC=∠ACB=45°,由此可得出BD,AC的长,进而根据题目给出的面积计算方法求出梯形的面积.
试题解析:(1)叙述:对角线互相垂直的四边形的面积等于对角线乘积的一半;
(2)过A,D分别作BC的垂线AE,DF,
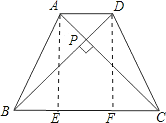
∵四边形ABCD为等腰梯形,
∵BD=AC,AB=CD,BC=BC
∴△ABC≌△DBC
∴∠ACB=∠DBC=45°,
在直角三角形BPC中,∠DBC=45°,BP=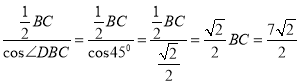 同理可得PD=
同理可得PD= ![]() ,BD=BP+PD=5
,BD=BP+PD=5![]() .
.
又等腰梯形对角线相等,即BD=AC=5![]() cm
cm
∴S梯形=![]() BDAC=25(cm2);
BDAC=25(cm2);


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )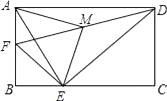
A.5
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:矩形ABCD的顶点B、C在x轴的正半轴上,A、D在抛物线![]() 上,矩形的顶点均为动点,且矩形在抛物线与
上,矩形的顶点均为动点,且矩形在抛物线与![]() 轴围成的区域里。
轴围成的区域里。
(1)设A点的坐标为(![]() ,
, ![]() ),试求矩形周长
),试求矩形周长![]() 关于变量
关于变量![]() 的函数表达式;
的函数表达式;
(2)是否存在这样的矩形,它的周长为9,试证明你的结论。
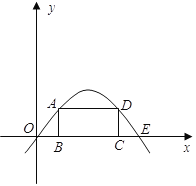
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
国际比赛的足球场长在100m到110m之间,宽在64m到75m之间,为了迎接2015年的亚洲杯,某地建设了一个长方形的足球场,其长是宽的1.5倍,面积是7560m2.请你判断这个足球场能用于国际比赛吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中O是原点,ABCD的顶点A,C的坐标分别是(8,0),(3,4),点D,E把线段OB三等分,延长CD、CE分别交OA、AB于点F,G,连接FG.则下列结论:
①F是OA的中点;②△OFD与△BEG相似;③四边形DEGF的面积是 ![]() ;④OD=
;④OD= ![]()
其中正确的结论是(填写所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究:
(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,探究MN与BM的数量关系,写出折叠方案,并结合方案证明你的结论.
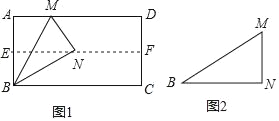
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在△ABC中,AO是BC边上的中线,AB与AC的“极化值”就等于AO2﹣BO2的值,可记为AB△AC=AO2﹣BO2 .
(1)在图1中,若∠BAC=90°,AB=8,AC=6,AO是BC边上的中线,则AB△AC= , OC△OA=;
(2)如图2,在△ABC中,AB=AC=4,∠BAC=120°,求AB△AC、BA△BC的值;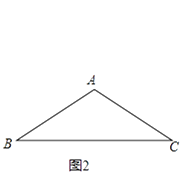
(3)如图3,在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON= ![]() AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com