
【题目】如图,已知AD∥BC,AB⊥BC,AB=BC=4,P为线段AB上一动点.将△BPC沿PC翻折至△EPC,延长CE交射线AD于点D
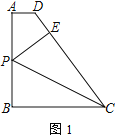
(1)如图1,当P为AB的中点时,求出AD的长
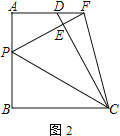
(2)如图2,延长PE交AD于点F,连接CF,求证:∠PCF=45°
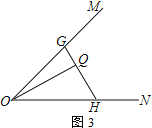
(3)如图3,∠MON=45°,在∠MON内部有一点Q,且OQ=8,过点Q作OQ的垂线GH分别交OM、ON于G、H两点.设QG=x,QH=y,直接写出y关于x的函数解析式
【答案】(1)1;(2)见解析;(3)![]()
【解析】
(1)如图1.根据平行线的性质得到∠A=∠B=90°,由折叠的性质得到∠CEP=∠B=90°,PB=PE,∠BPC=∠EPC,根据全等三角形的性质得到∠APD=∠EPD,推出![]() 于是得到结论;
于是得到结论;
(2)如图2.过C作CG⊥AF交AF的延长线于G,推出四边形ABCG是矩形,得到矩形ABCG是正方形,求得CG=CB,根据折叠的性质得到∠CEP=∠B=90°,BC=CE,∠BCP=∠ECP, 根据全等三角形的性质即可得到结论:
(3)如图3,将△OQG沿OM翻折至△OPG,将△OQH沿ON翻折至△ORH,延长PG, RH交于S,推出四边形PORS是正方形,根据勾股定理即可得到结论.
解:(1)如图1,连结![]() ,
,
∵AD//BC. AB⊥BC,
∴∠A=∠B=90°
∵将△BPC沿PC翻折至△EPC,
∴∠CEP=∠B=90°,PB=PE,∠BPC=∠EPC,
∴∠DEP=90°
∵当P为AB的中点,
∴AP=BP
∴PA=PE
∵PD=PD
∴![]() ,
,
∴![]()
作![]() 于
于![]() ,设
,设![]() ,则
,则![]() ,
,![]()
由勾股定理得![]() ,
,
解得![]() ,
,
∴![]()
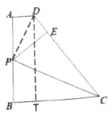
图1
(2)如图2,作![]() 交延长线于
交延长线于![]() ,易证四边形
,易证四边形![]() 为正方形
为正方形
∵∠A=∠B=∠G=90°,
∴四边形ABCG是矩形,
∵AB=BC,
∴矩形ABCG是正方形,
∴CG=CB.
∵将△BPC沿PC翻折至△EPC,
∴∠ FED=90°,CG=CE,
又∵CF=CF
∴![]() ,
,
∴∠ECF=∠GCF,
∴∠BCP+∠GCF=∠PCE+∠FCE=45°
∴∠PCF=45°;
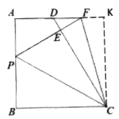
图2/p>
(3)如图3.将△OQG沿OM翻折至OOPG.将△OQH沿ON翻折至△ORH.延长PG, RH交于S,则∠POG=∠QOG.∠ROH=∠QOH, OP=OQ=OR=8,PG=QG=x,QH=RH=y,
∴ ∠POR=2∠MON=90",
∵GH⊥OQ.
∴∠OQG=∠OQH=90° .
∴∠P=∠R=90° ,
∴四边形PORS是正方形。
∴PS=RS=8,∠S=90°,
∴.GS=8-x,HS=8-y.
∴![]() .
.
∴ ![]()
∴![]()
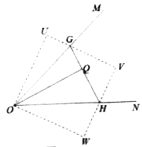
图3


科目:初中数学 来源: 题型:
【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
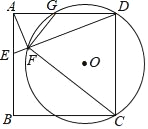
【题目】如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.
(1)求证:△AFG∽△DFC;
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
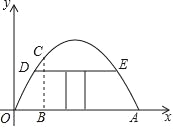
【题目】有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示,已知OA=8米,距离O点2米处的棚高BC为![]() 米.
米.
(1)求该抛物线的解析式;
(2)若借助横梁DE(DE∥OA)建一个门,要求门的高度为1.5米,求横梁DE的长度是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制第二条边长只能比第一条边长的3倍少2米.
(1)用含m的式子表示第三条边长;
(2)第一条边长能否为10米?为什么?
(3)若第一条边长最短,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为Rt△ABC的直角边AC上一点,以OC为半径的圆与斜边AB相切于点D,P是弧CD上任意一点,过点P作⊙O的切线,交BC于点M,交AB于点N,已知AB=5,AC=4.
(1)△BMN的周长等于多少;
(2)⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列五条结论: ①abc<0;②4ac-b2<0;③4a+c<2b;④3b+2c<0;⑤m(am+b)+b<a(m≠-1).其中正确的结论是_________(把所有正确的结论的序号都填写在横线上)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com