
【题目】已知:PA、PB、CD分别切⊙O于A、B、E三点,PA=6.求:
(1)△PCD的周长;
(2)若∠P=50°,求∠COD的度数.
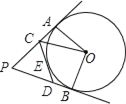
【答案】(1)12;(2) 65°.
【解析】
(1)根据切线长定理,即可得到PA=PB,ED=AD,CE=BC,从而求得三角形的周长=2PA;
(2)连接OE,根据切线的性质得出∠P+∠AOB=180°,由切线长定理得∠COD= ![]() ∠AOB,即可得出结果.
∠AOB,即可得出结果.
解:(1)∵PA、PB切⊙O于A、B,CD切⊙O于E,
∴PA=PB=6,ED=AD,CE=BC;
∴△PCD的周长=PD+DE+PC+CE=2PA=12;
(2)连接OE,如图所示:
由切线的性质得,OA⊥PA,OB⊥PB,OE⊥CD,
∴∠OAC=∠OEC=∠OED=∠OBD=90°,
∴∠AOB+∠P=180°,
∴∠AOB=180°﹣∠P=130°,
由切线长定理得:∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=![]() ∠AOB=
∠AOB=![]() ×130°=65°.
×130°=65°.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】一袋装有编号为1,2,3的三个形状、大小、材质等相同的小球,从袋中随意摸出1个球,记事件A为“摸出的球编号为奇数”,随意抛掷一个之地均匀正方体骰子,六个面上分别写有1﹣6这6个整数,记事件B为“向上一面的数字是3的整数倍”,请你判断等式“P(A)=2P(B)”是否成立,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D、E分别在BC、AC上,且CD=2BD,AE=2CE,BE、AD相交于点F,连接DE,则下列结论:
①∠AFE=60°;②DE⊥AC;③CE2=DFDA;④AFBE=AEAC,正确的结论有( )
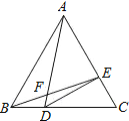
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
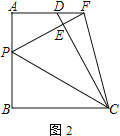
【题目】如图,已知AD∥BC,AB⊥BC,AB=BC=4,P为线段AB上一动点.将△BPC沿PC翻折至△EPC,延长CE交射线AD于点D
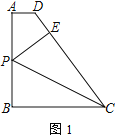
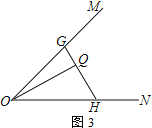
(1)如图1,当P为AB的中点时,求出AD的长
(2)如图2,延长PE交AD于点F,连接CF,求证:∠PCF=45°
(3)如图3,∠MON=45°,在∠MON内部有一点Q,且OQ=8,过点Q作OQ的垂线GH分别交OM、ON于G、H两点.设QG=x,QH=y,直接写出y关于x的函数解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经市场调研发现:某品牌童装平均每天可售出 20 件,每件盈利 40元.在每件降价幅度不超过 18 元的情况下,若每件童装降价 1 元,则每天可多售出 2 件,设降价 x 元.
(1)降价 x 元后,每件童装盈利是多少元,每天销售量是多少件;
(2)要想每天销售这种童装盈利 1200 元,那么每件童装应降价多少元?
(3)每天能盈利 1800 元吗?如果能,每件童装应降价多少元?如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
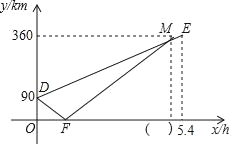
【题目】A,B,C三地在同一条公路上,A地在B,C两地之间,甲、乙两车同时从A地出发匀速行驶,甲车驶向C地,乙车先驶向B地,到达B地后,调头按原速经过A地驶向C地(调头时间忽略不计),到达C地停止行驶,甲车比乙车晚0.4小时到达C地,两车距B地的路程y(km)与行驶时间x(h)之间的函数关系如图所示,请结合图象信息,解答下列问题:
(1)甲车行驶的速度是 km/h,并在图中括号内填入正确的数值;
(2)求图象中线段FM所表示的y与x的函数解析式(不需要写出自变量x的取值范围);
(3)在乙车到达C地之前,甲、乙两车出发后几小时与A地路程相等?直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
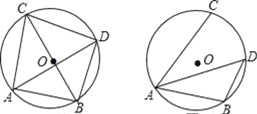
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com