
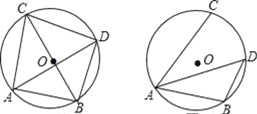
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
【答案】(1)AC=8,BD=CD=5![]() ;(2)5.
;(2)5.
【解析】
试题(Ⅰ)利用圆周角定理可以判定△CAB和△DCB是直角三角形,利用勾股定理可以求得AC的长度;利用圆心角、弧、弦的关系推知△DCB也是等腰三角形,所以利用勾股定理同样得到BD=CD=5![]() ;
;
(Ⅱ)如图②,连接OB,OD.由圆周角定理、角平分线的性质以及等边三角形的判定推知△OBD是等边三角形,则BD=OB=OD=5.
试题解析:(Ⅰ)如图①,∵BC是⊙O的直径,
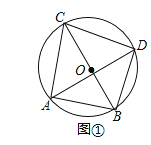
∴∠CAB=∠BDC=90°.
∵在直角△CAB中,BC=10,AB=6,
∴由勾股定理得到:AC=![]() .
.
∵AD平分∠CAB,
∴![]() ,
,
∴CD=BD.
在直角△BDC中,BC=10,CD2+BD2=BC2,
∴易求BD=CD=5![]() ;
;
(Ⅱ)如图②,连接OB,OD.
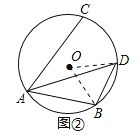
∵AD平分∠CAB,且∠CAB=60°,
∴∠DAB=![]() ∠CAB=30°,
∠CAB=30°,
∴∠DOB=2∠DAB=60°.
又∵OB=OD,
∴△OBD是等边三角形,
∴BD=OB=OD.
∵⊙O的直径为10,则OB=5,
∴BD=5.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
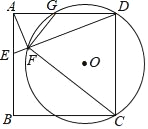
【题目】如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.
(1)求证:△AFG∽△DFC;
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为Rt△ABC的直角边AC上一点,以OC为半径的圆与斜边AB相切于点D,P是弧CD上任意一点,过点P作⊙O的切线,交BC于点M,交AB于点N,已知AB=5,AC=4.
(1)△BMN的周长等于多少;
(2)⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表所示.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
下列说法:①抛物线与y轴的交点为(0,6); ②抛物线的对称轴在y轴的右侧;③抛物线一定经过点(3,0);④在对称轴左侧,y随x增大而减小.⑤不等式ax2+(b﹣3)x+c﹣6>0解集为﹣2<x<0.其中说法正确的有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则弧AD的长为( )
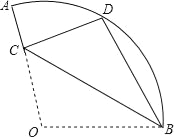
A. 2π B. 3π C. 4π D. 5π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图乙,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)如图甲,将△ADE绕点A 旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是_____.
①BD=CE②BD⊥CE③∠ACE+∠DBC=45°④BE2=2(AD2+AB2)
(2)若AB=4,AD=2,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②求旋转过程中线段PB长的最大值.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列五条结论: ①abc<0;②4ac-b2<0;③4a+c<2b;④3b+2c<0;⑤m(am+b)+b<a(m≠-1).其中正确的结论是_________(把所有正确的结论的序号都填写在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=﹣![]() x2,当水位上涨1m时,水面宽CD为2
x2,当水位上涨1m时,水面宽CD为2![]() m,则桥下的水面宽AB为_____m.
m,则桥下的水面宽AB为_____m.
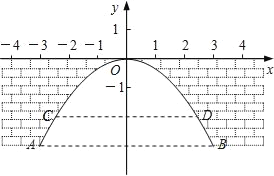
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com