
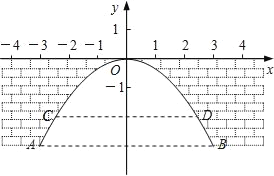
【题目】在如图所示的平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=﹣![]() x2,当水位上涨1m时,水面宽CD为2
x2,当水位上涨1m时,水面宽CD为2![]() m,则桥下的水面宽AB为_____m.
m,则桥下的水面宽AB为_____m.
科目:初中数学 来源: 题型:
【题目】如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:
①∠BAD=2∠F;②∠E+∠F=90°
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:(1)AD∥BC.理由如下:
∵∠ADE+∠ADF=180°,(平角的定义)
∠ADE+∠BCF=180°,(已知)
∴∠ADF=∠________,(________)
∴AD∥BC
(2)AB与EF的位置关系是:________.
∵BE平分∠ABC,(已知)
∴∠ABE=![]() ∠ABC.(角平分线的定义)
∠ABC.(角平分线的定义)
又∵∠ABC=2∠E,(已知),
即∠E=![]() ∠ABC,
∠ABC,
∴∠E=∠________.(________)
∴________∥________.(________)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1, B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2017,最少经过多少次操作 ( )

A. 4B. 5C. 6D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从![]() 两地同时出发,相向而行.快车到达
两地同时出发,相向而行.快车到达![]() 地后,停留3秒卸货,然后原路返回
地后,停留3秒卸货,然后原路返回![]() 地,慢车到达
地,慢车到达![]() 地即停运休息,如图表示的是两车之间的距离
地即停运休息,如图表示的是两车之间的距离![]() (米)与行驶时间
(米)与行驶时间![]() (秒)的函数图象,根据图象信息,计算
(秒)的函数图象,根据图象信息,计算![]() 的值分别为( )
的值分别为( )
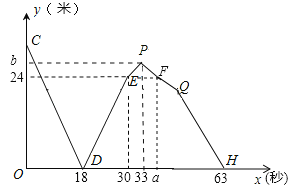
A. 39,26B. 39,26.4C. 38,26D. 38,26.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,可以求代数式的最大值或最小值等.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,可以求代数式的最大值或最小值等.
例如:求代数式![]() 的最小值
的最小值![]() .
.
![]() 当
当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() .
.
根据阅读材料用配方法解决下列问题:
(1)当![]() 为何值时,代数式
为何值时,代数式![]() 有最小值,求出这个最小值.
有最小值,求出这个最小值.
(2)当![]() ,
,![]() 为什么关系时,代数式
为什么关系时,代数式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
(3)当![]() ,
,![]() 为何值时,多项式
为何值时,多项式![]() 有最大值,并求出这个最大值.
有最大值,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,顶点全在格点上的多边形为“格点多边形”.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如,图中三角形ABC是格点三角形,其中S=2,N=0,L=6.

(1)图中格点多边形DEFGHI所对应的S= ,N= ,L= .
(2)经探究发现,任意格点多边形的面积S可表示为S=aN+bL﹣1,其中a,b为常数
①试求a,b的值.(提示:列方程组)
②求当N=5,L=14时,S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠B和∠C的平分线相交于点F.

(1)若∠A=60°,试求∠BFC的度数;
(2)过点F作DE∥BC交AB于D,交AC于E,若DE=9,求线段BD+CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com