练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，已知∠B和∠C的平分线相交于点F.

    (1)若∠A=60°，试求∠BFC的度数；

    (2)过点F作DE∥BC交AB于D，交AC于E，若DE=9，求线段BD+CE的长.

    【答案】（1）120° （2）9

    【解析】

    （1）利用角平分线的定义及三角形的内角和定理即可求解.

    （2）利用两直线平行，内错角相等，角平分线的定义以及三角形中等角对等边的性质进行求解即可．

    （1）∵∠A+∠ABC+∠ACB=180°，∠A=60°

    ∴∠ABC+∠ACB=120°

    ∵BF平分∠ABC，CF平分∠ACB

    ∴∠FBC=∠ABC， ∠BCF=∠ACB

    ∴∠FBC+∠BCF=（∠ABC+∠ACB）=60°

    ∴∠BFC=180°-（∠FBC+∠BCF）=120°

    （2）如图所示：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图,四边形ABCD是正方形,点E、K分别在BC、AB上,CE=BK,点G在BA的延盖

    长线上,且DG⊥DE.

    (1)如图(1)求证:CK=DG；

    (2)如图(2)不添加任何辅助线的条件下,直接写出图中所有的与四边形BEDK面积相等

    的三角形。

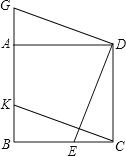
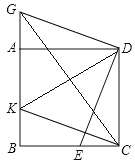
    图1 图2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

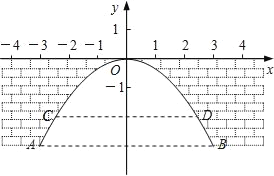
    【题目】在如图所示的平面直角坐标系中，桥孔抛物线对应的二次函数关系式是y＝﹣x2，当水位上涨1m时，水面宽CD为2m，则桥下的水面宽AB为_____m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】工人小王生产甲、乙两种产品，生产产品件数与所用时间之间的关系如表：

    生产甲产品件数（件）

    生产乙产品件数（件）

    所用总时间（分钟）

    10

    10

    350

    30

    20

    850

    （1）小王每生产一件甲种产品和每生产一件乙种产品分别需要多少分钟？

    （2）小王每天工作8个小时，每月工作25天．如果小王四月份生产甲种产品a件（a为正整数）．

    ①用含a的代数式表示小王四月份生产乙种产品的件数；

    ②已知每生产一件甲产品可得1.50元，每生产一件乙种产品可得2.80元，若小王四月份的工资不少于1500元，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC的顶点A在原点，B、C坐标分别为B（3，0），C（2，2），将△ABC向左平移1个单位后再向下平移2单位，可得到△A′B′C′．

    （1）请画出平移后的△ABC的图形

    （2）写出△A′B′C′各个顶点的坐标；

    （3）在x轴上是否存在点P，值，若存在，请写出P点的坐标，若不存在请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AC＝BC，∠ACB＝90°，AE平分∠BAC，BF⊥AE，交AC的延长线于F，且垂足为E，则下列结论：①AD＝BF；②BF＝AF；③AC＋CD＝AB；④AB＝BF；⑤AD＝2BE，其中正确的结论有( )个.

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点，若点D为BC边的中点，点M为线段EF上一动点，则周长的最小值为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系xOy中的点P（a，b），若点P′的坐标为（a+kb，ka+b）（其中k为常数，且k≠0），

    则称点P′为点P的“k属派生点”．例如：P（1，4）的“2属派生点”为P′（1+2×4，2×1+4），即P′（9，6）．

    （Ⅰ）点P（﹣2，3）的“3属派生点”P′的坐标为　 　；

    （Ⅱ）若点P的“5属派生点”P′的坐标为（3，﹣9），求点P的坐标；

    （Ⅲ）若点P在x轴的正半轴上，点P的“k属派生点”为P′点，且线段PP′的长度为线段OP长度的2倍，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】山地自行车越来越受到中学生的喜爱，各种品牌相继投放市场，某车行经营的A型车去年销售总额为5万元，今年每辆销售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少20%．

    （1）今年A型车每辆售价多少元？（用列方程的方法解答）

    （2）该车行计划新进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？

    A，B两种型号车的进货和销售价格如下表：

    A型车

    B型车

    进货价格（元）

    1100

    1400

    销售价格（元）

    今年的销售价格

    2000

    查看答案和解析>>

    同步练习册答案