Question

【题目】如图,四边形ABCD是正方形,点E、K分别在BC、AB上,CE=BK,点G在BA的延盖

长线上,且DG⊥DE.

(1)如图(1)求证:CK=DG；

(2)如图(2)不添加任何辅助线的条件下,直接写出图中所有的与四边形BEDK面积相等

的三角形。

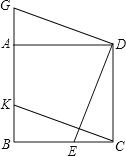
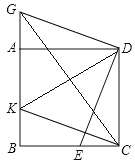
图1 图2

Answer 1

【答案】（1）证明见解析；（2）ΔGKD,ΔCKD,ΔKGC,ΔDGC.

【解析】试题分析：（1）依据正方形的性质，判定△DCE≌△CBK，即可得到DE=CK，再判定△ADG≌△CDE，即可得到DG=DE，进而得出DG=CK；

（2）依据△DCE≌△CBK，可得S△DCE=S△BCK，进而得到S四边形BEFK=S△CDF，进而得出S四边形BEDK=S△CDK，再根据四边形CDGK是平行四边形，即可得到S△CDK=S△CDG=S△GDK=S△CGK．

试题解析：解：（1）如图1．∵四边形ABCD是正方形，∴DC=CB=AD，∠B=∠DCE=∠DAG=90°．∵CE=BK，∴△DCE≌△CBK，∴DE=CK．∵DG⊥DE，∴∠ADG+∠ADE=90°=∠CDE+∠ADE，∴∠ADG=∠CDE．又∵∠DAG=∠DCE=90°，AD=CD，∴△ADG≌△CDE，∴DG=DE，∴DG=CK；

（2）如图2．∵△DCE≌△CBK，∴S△DCE=S△BCK，∴S四边形BEFK=S△CDF，∴S四边形BEFK+S△DFK=S△CDF+S△DFK，即S四边形BEDK=S△CDK．∵△ADG≌△CDE，∴CE=BK=AG，∴CD=AB=GK．又∵DG=CK，∴四边形CDGK是平行四边形，∴S△CDK=S△CDG=S△GDK=S△CGK，∴与四边形BEDK面积相等的三角形为△CDK，△CDG，△GDK，△GCK．