
【题目】在等边△ABC中.
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②求证:PA=PM.

【答案】(1)80°(2)①见解析(2)证明见解析
【解析】
(1)根据等边三角形的性质得到∠B=60°,由三角形的外角等于不相邻的两个内角和得出∠APC的度数,再由等边对等角即可得出结论;
(2)①根据题意补全图形;
②证明△APM为等边三角形即可得出结论.
(1)∵△ABC为等边三角形,∴∠B=60°,∴∠APC=∠BAP+∠B=80°.
∵AP=AQ,∴∠AQB=∠APC=80°.
(2)① 补全图形如图所示.

②过点A作AH⊥BC于点H,如图,∵△ABC为等边三角形,AP=AQ,∴∠PAH=∠QAH,∠BAH=∠CAH,∴∠PAB=∠QAC.
∵点Q,M关于直线AC对称,∴∠QAC=∠MAC,AQ=AM,∴∠PAB=∠MAC,AP=AM.
∵∠BAC=60°,∴∠PAM=∠BAC=60°.
∵AP=AM,∴△APM为等边三角形,∴PA=PM.


科目:初中数学 来源: 题型:
【题目】小明、小丽两位同学学习数学都养成了良好的预习习惯.某天他俩预习了课本第107页上的问题3,题目如下:
某小组计划做一批“中国结”,如果每人做5个,那么比计划多了9个;如果每人做4个,那么比计划少15个.该小组共有多少人?计划做多少个“中国结”?
他俩都没有看课本上的解答过程,而是独立思考,分别列出了如下尚不完整的方程:
小明:![]() ; 小丽:
; 小丽:![]() .
.
(1)在小明、小丽所列的方程中,“□”中是运算符号,“( )”中是数字,试分别指出未知数![]() 、
、![]() 表示的意义;
表示的意义;
(2)试选择一种方法,将问题3解答完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在等边△ABC中, AB= ![]() ,D,E分别是AB,BC的中点(如图1).若将△BDE绕点B逆时针旋转,得到△BD1E1 , 设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.
,D,E分别是AB,BC的中点(如图1).若将△BDE绕点B逆时针旋转,得到△BD1E1 , 设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.
(1)判断△BDE的形状;
(2)在图2中补全图形,
①猜想在旋转过程中,线段CE1与AD1的数量关系并证明;
②求∠APC的度数;
(3)点P到BC所在直线的距离的最大值为 . (直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数. ![]() ,
, ![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数 ![]() 的图象与性质.
的图象与性质.
小慧根据学习函数的经验,对函数 ![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小慧的探究过程,请补充完成:
(1)函数 ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)列出y与x的几组对应值.请直接写出m的值,m=;
x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
(3)请在平面直角坐标系 ![]() , 描出以上表中各对对应值为坐标的点,并画出该函数的图象;
, 描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出该函数的两条性质:
①;
② .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=﹣x+10在第一象限内一个动点.
(1)求△OPA的面积S与x的函数关系式,并写出自变量的x的取值范围;
(2)当△OPA的面积为10时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
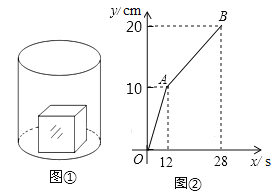
【题目】(2017·吉林)如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
(1)正方体的棱长为 cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为![]() ,C点的坐标为
,C点的坐标为![]() ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着![]() 的路线移动
的路线移动![]() 即:沿着长方形移动一周
即:沿着长方形移动一周![]() .
.
![]() 写出点B的坐标
写出点B的坐标![]() ______
______![]()
![]() 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
![]() 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com