
【题目】如图,四边形ABCD是![]() 的内接四边形,
的内接四边形,![]() .
.
![]() 如图
如图![]() ,求证:
,求证:![]() ;
;
![]() 如图
如图![]() ,点F是AC的中点,弦
,点F是AC的中点,弦![]() ,交BC于点E,交AC于点M,求证:
,交BC于点E,交AC于点M,求证:![]() ;
;
![]() 在
在![]() 的条件下,若DG平分
的条件下,若DG平分![]() ,
,![]() ,
,![]() ,求
,求![]() 的半径.
的半径.

【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
![]() 由
由![]() ,得到
,得到![]() ,从而得到
,从而得到![]() ,即可得到
,即可得到![]() .
.
![]() 如图2,延长AD到N,使
如图2,延长AD到N,使![]() ,连接NC,构造三角形中位线和全等三角形
,连接NC,构造三角形中位线和全等三角形![]() ≌
≌![]() ,由该全等三角形的对应边相等得到:
,由该全等三角形的对应边相等得到:![]() 所以
所以![]() ,即
,即![]() ;
;
![]() 如图3,连接BG,过点A作
如图3,连接BG,过点A作![]() ,构造等边三角形
,构造等边三角形![]() 、
、![]() 通过
通过![]() 得
得![]() ,
,![]() ,
,![]() ,
,![]() 作直径AP,连接CP,
作直径AP,连接CP,![]() ,故
,故![]() ,由锐角三角函数的定义求得
,由锐角三角函数的定义求得![]() ,从而得到直径AP的长度,易得半径的长度.
,从而得到直径AP的长度,易得半径的长度.
(1)如图1,连接AC,
![]() ,
,
![]() ,
,
![]() ;
;

![]() 如图2,延长AD到N,使
如图2,延长AD到N,使![]() ,连接NC,
,连接NC,

![]() ,
,![]() ,
,
![]() 四边形ABED是平行四边形,
四边形ABED是平行四边形,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,
![]() ;
;
![]() 如图3,连接BG,过点A作
如图3,连接BG,过点A作![]() ,
,

由![]() 知
知![]() ,
,
四边形ABED是平行四边形,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,∠NDC=∠DCE,
,∠NDC=∠DCE,
![]() ,
,
![]() ,
,![]() ,
,
∴∠DEC=∠DCE=∠EDC,
∴△CDE是等边三角形,
∴∠DEC=∠DCE=∠EDC=60°,DE=CE,
∵∠BGE=∠BCD=60°,∠BEG=∠DEC=60°,
∴![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() 解
解![]() 得
得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
作直径AP,连接CP,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 的半径是
的半径是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB,CF⊥AD.试说明:
(1)△CBE≌△CDF;
(2)AB+DF=AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)求证:MN=AM+BN.
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有点A(a+1,2),B(-a-5,2a+1).
(1)若线段AB∥y轴,求点A、B的坐标;
(2)当点B到y轴的距离是到x轴的距离4倍时,求点B所在的象限位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E、K分别在BC、AB上,CE=BK,点G在BA的延盖
长线上,且DG⊥DE.
(1)如图(1)求证:CK=DG;
(2)如图(2)不添加任何辅助线的条件下,直接写出图中所有的与四边形BEDK面积相等
的三角形。
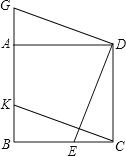
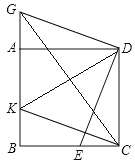
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①平方等于其本身的数有0,±1;②32xy3是4次单项式;③将方程![]() 中的分母化为整数,得
中的分母化为整数,得![]() =12;④平面内有4个点,过每两点画直线,可画6条、4条或1条.其中正确的有( )
=12;④平面内有4个点,过每两点画直线,可画6条、4条或1条.其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)已知购买1个足球和1个篮球共需130元,购买2个足球和1个篮球共需180元.
(1)求每个足球和每个篮球的售价;
(2)如果某校计划购买这两种球共54个,总费用不超过4000元,问最多可买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC=BC,∠ACB=90°,AE平分∠BAC,BF⊥AE,交AC的延长线于F,且垂足为E,则下列结论:①AD=BF;②BF=AF;③AC+CD=AB;④AB=BF;⑤AD=2BE,其中正确的结论有( )个.

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com