
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)求证:MN=AM+BN.
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.
【答案】(1)见解析;(2)MN=BN-AM.理由见解析;
【解析】
(1)利用互余关系证明∠MAC=∠NCB,又∠AMC=∠CNB=90°,AC=BC,故可证△AMC≌△CNB,从而有AM=CN,MC=BN,利用线段的和差关系证明结论;
(2)类似于(1)的方法,证明△AMC≌△CNB,从而有AM=CN,MC=BN,可推出AM、BN与MN之间的数量关系.
(1)∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中
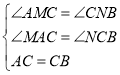 ,
,
△AMC≌△CNB(AAS),
AM=CN,MC=NB,
∵MN=NC+CM,
∴MN=AM+BN;
(2)结论:MN=BN-AM.
∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,
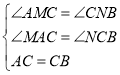 ,
,
△AMC≌△CNB(AAS),
AM=CN,MC=NB,
∵MN=CM-CN,
∴MN=BN-AM.


科目:初中数学 来源: 题型:
【题目】某中学计划购买A型和B型课桌凳共200套. 经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,且购买4套A型和5套B型课桌凳共需1820元.(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)、学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在街头巷尾会遇到一类“摸球游戏”,摊主把分别标有数字1,2,3的3个白球和标有数字4,5,6的3个黑球放在口袋里![]() 球除颜色外,其他均相同
球除颜色外,其他均相同![]() ,让你摸球
,让你摸球![]() 规定:每付3元钱就玩一局,每局连续摸两次,每次只能摸一个,第一次摸完后把球放回口袋里搅匀后再摸一次,若前后两次摸得的都是白球,摊主就送你10元钱的奖品.
规定:每付3元钱就玩一局,每局连续摸两次,每次只能摸一个,第一次摸完后把球放回口袋里搅匀后再摸一次,若前后两次摸得的都是白球,摊主就送你10元钱的奖品.
![]() 用列表法或树状图表示摸出的两个球可能出现的所有结果;
用列表法或树状图表示摸出的两个球可能出现的所有结果;
![]() 求获奖的概率.
求获奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:
①∠BAD=2∠F;②∠E+∠F=90°
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:(1)AD∥BC.理由如下:
∵∠ADE+∠ADF=180°,(平角的定义)
∠ADE+∠BCF=180°,(已知)
∴∠ADF=∠________,(________)
∴AD∥BC
(2)AB与EF的位置关系是:________.
∵BE平分∠ABC,(已知)
∴∠ABE=![]() ∠ABC.(角平分线的定义)
∠ABC.(角平分线的定义)
又∵∠ABC=2∠E,(已知),
即∠E=![]() ∠ABC,
∠ABC,
∴∠E=∠________.(________)
∴________∥________.(________)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做投掷骰子(质地均匀的正方体)实验,共做了50次试验,将记录的数据进行整理,绘制了如下的统计表:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 8 |
| 9 | 9 | 7 |
频率 | 0.14 |
| 0.20 | 0.18 | 0.18 | 0.14 |
(1)上表中,![]() =______,
=______,![]() =_______.
=_______.
(2)正在做掷骰子实验的小颖和小明准备做一个游戏:两人分别掷一次骰子,谁掷出的骰子朝上的点数最大谁就获胜.现小明先掷,掷出的点数为4,请分别求出小明与小颖获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中.
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②求证:PA=PM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是![]() 的内接四边形,
的内接四边形,![]() .
.
![]() 如图
如图![]() ,求证:
,求证:![]() ;
;
![]() 如图
如图![]() ,点F是AC的中点,弦
,点F是AC的中点,弦![]() ,交BC于点E,交AC于点M,求证:
,交BC于点E,交AC于点M,求证:![]() ;
;
![]() 在
在![]() 的条件下,若DG平分
的条件下,若DG平分![]() ,
,![]() ,
,![]() ,求
,求![]() 的半径.
的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,可以求代数式的最大值或最小值等.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,可以求代数式的最大值或最小值等.
例如:求代数式![]() 的最小值
的最小值![]() .
.
![]() 当
当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() .
.
根据阅读材料用配方法解决下列问题:
(1)当![]() 为何值时,代数式
为何值时,代数式![]() 有最小值,求出这个最小值.
有最小值,求出这个最小值.
(2)当![]() ,
,![]() 为什么关系时,代数式
为什么关系时,代数式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
(3)当![]() ,
,![]() 为何值时,多项式
为何值时,多项式![]() 有最大值,并求出这个最大值.
有最大值,并求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com