
【题目】如图,平面直角坐标系中,A(﹣3,﹣2)、B(﹣1,﹣4)
(1)直接写出:S△OAB= ;
(2)延长AB交y轴于P点,求P点坐标;
(3)Q点在y轴上,以A、B、O、Q为顶点的四边形面积为6,求Q点坐标.

【答案】(1)5;(2)(0,﹣5);(3) (0, ![]() )或(0,﹣2).
)或(0,﹣2).
【解析】试题解析:(1)延长AB交y轴于P点,如图,利用待定系数法求出直线AB的解析式为y=-x-5,则得到P(0,-5),然后根据三角形面积公式和利用S△OAB=S△AOP-S△OBP进行计算即可;
(2)由(1)得到P点的坐标;
(3)分类讨论:当Q在y轴的正半轴上时,利用S四边形ABOQ=S△AOB+S△AOQ得到S△AOQ=1,再根据三角形面积公式求出OQ.从而得到Q点坐标;当Q在y轴的负半轴上时,利用S四边形ABOQ=S△AOB+S△BOQ得到S△BOQ=1,再根据三角形面积公式求出OQ.从而得到Q点坐标.
试题解析:(1)延长AB交y轴于P点,如图,
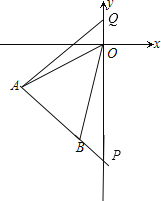
设直线AB的解析式为y=kx+b,
把A(﹣3,﹣2)、B(﹣1,﹣4)代入得![]()
解得![]() .
.
所以直线AB的解析式为y=﹣x﹣5,
当x=0时,y=﹣x﹣5=﹣5,则P(0,﹣5),
所以S△OAB=S△AOP﹣S△OBP
=![]() ×5×3﹣
×5×3﹣![]() ×5×1
×5×1
=5.
(2)由(1)得到P点的坐标为(0,﹣5);
(3)当Q在y轴的正半轴上时,∵S四边形ABOQ=S△AOB+S△AOQ,
∴S△AOQ=6﹣5=1,
∴![]() ×3×OQ=1,
×3×OQ=1,
解得OQ=![]() .
.
则此时Q点的坐标为(0, ![]() );
);
当Q在y轴的负半轴上时,
∵S四边形ABOQ=S△AOB+S△BOQ,
∴S△BOQ=1,
∴S△AOQ=6﹣5=1,
∴![]() ×1×OQ=1,
×1×OQ=1,
解得OQ=2,
则此时Q点的坐标为(0,﹣2),
即Q点坐标为(0, ![]() )或(0,﹣2).
)或(0,﹣2).


科目:初中数学 来源: 题型:
【题目】平面直角坐标系内的一条直线同时满足下列两个条件:①不经过第四象限;②与两条坐标轴所围成的三角形的面积为2,这条直线的解析式可以是_________(写出一个解析式即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利25%元,则这件商品的进价为_______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )
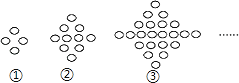
A.190 B.94 C.70 D.46
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋时期杰出的数学家杨辉是钱塘人,下面的图表是他在《详解九章算术》中记载的“杨辉三角”.此图揭示了![]() (为非负整数)的展开式的项数及各项系数的有关规律.
(为非负整数)的展开式的项数及各项系数的有关规律.
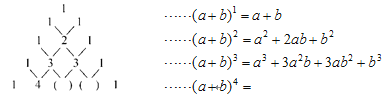
(1)请仔细观察,填出(a+b)4的展开式中所缺的系数.(a+b)4=a4+4a3b+_____a2b2+4ab2+b4
(2)此规律还可以解决实际问题:假如今天是星期三,再过7天还是星期三,那么再过![]() 天是星期____.
天是星期____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com