
【题目】如图,△ABC是等边三角形,点D、E分别在BC、AC上,且CD=2BD,AE=2CE,BE、AD相交于点F,连接DE,则下列结论:
①∠AFE=60°;②DE⊥AC;③CE2=DFDA;④AFBE=AEAC,正确的结论有( )
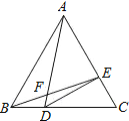
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
【答案】D
【解析】
本题是开放题,对结论进行一一论证,从而得到答案.①利用△ABD≌△BCE,再用三角形的一个外角等于与它不相邻的两个内角和,即可证∠AFE=60°;②从CD上截取CM=CE,连接EM,证△CEM是等边三角形,可证明DE⊥AC;③△BDF∽△ADB,由相似比则可得到CE2=DFDA;④只要证明了△AFE∽△BAE,即可推断出AFBE=AEAC.
∵△ABC是等边三角形
∴AB=BC=AC,∠BAC=∠ABC=∠BCA=60°
∵BD= ![]() BC,CE=
BC,CE= ![]() AC
AC
∴BD=CE.
∴△ABD≌△BCE
∴∠BAD=∠CBE,
∵∠ABE+∠EBD=60°
∴∠ABE+∠CBE=60°
∵∠AFE是△ABF的外角
∴∠AFE=60°
∴①是对的;
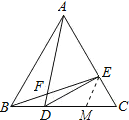
如图,从CD上截取CM=CE,连接EM,则△CEM是等边三角形
∴EM=CM=EC
∵EC= ![]() CD
CD
∴EM=CM=DM
∴∠CED=90°
∴DE⊥AC,
∴②是对的;
由前面的推断知△BDF∽△ADB
∴BD:AD=DF:DB
∴BD2=DFDA
∴CE2=DFDA
∴③是对的;
在△AFE和△BAE中,∠BAE=∠AFE=60°,∠AEB是公共角
∴△AFE∽△BAE
∴AFBE=AEAC
∴④是对的;
故答案为:D.


科目:初中数学 来源: 题型:
【题目】如图,市防汛指挥部决定对某水库的水坝进行加高加固,设计师提供的方案是:水坝加高1米(EF=1米),背水坡AF的坡度i=1∶1,已知AB=3米,∠ABE=120°,求水坝原来的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
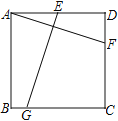
【题目】如图,在边长为6的正方形ABCD中,点F为CD上一点,E是AD的中点,且DF=2.在BC上找点G,使EG=AF,则BG的长是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
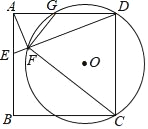
【题目】如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.
(1)求证:△AFG∽△DFC;
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高铁给我们的出行带来了极大的方便.如图,“和谐号”高铁列车座椅后面的小桌板收起时,小桌板的支架的底端N与桌面顶端M的距离MN=75cm,且可以看作与地面垂直.展开小桌板使桌面保持水平,AB⊥MN,∠MAB=∠MNB=37°,且支架长BN与桌面宽AB的长度之和等于MN的长度.求小桌板桌面的宽度AB(结果精确到1cm,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
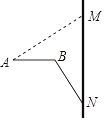
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示,已知OA=8米,距离O点2米处的棚高BC为![]() 米.
米.
(1)求该抛物线的解析式;
(2)若借助横梁DE(DE∥OA)建一个门,要求门的高度为1.5米,求横梁DE的长度是多少米?
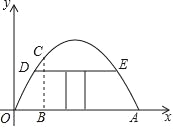
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图乙,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)如图甲,将△ADE绕点A 旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是_____.
①BD=CE②BD⊥CE③∠ACE+∠DBC=45°④BE2=2(AD2+AB2)
(2)若AB=4,AD=2,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②求旋转过程中线段PB长的最大值.




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com