
【题目】边长分别为6、8、10的三角形的内切圆半径是_____,外接圆半径是_____.
【答案】2, 5
【解析】
先根据勾股定理的逆定理判断出△ABC的形状,设△ABC内切圆的半径为R,切点分别为D、E、F,再根据题意画出图形,先根据正方形的判定定理判断出四边形ODCE是正方形,再根据切线长定理即可得到关于R的一元一次方程,求出R的值即可,再根据直角三角形的外接圆的半径是斜边的一半,得其半径即可.
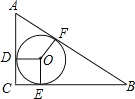
如图所示:△ABC中,AC=6,BC=8,AB=10,
∵62+82=102,即AC2+BC2=AB2,
∴△ABC是直角三角形,
设△ABC内切圆的半径为R,切点分别为D. E.F,
∵CD=CE,BE=BF,AF=AD,
∵OD⊥AC,OE⊥BC,
∴四边形ODCE是正方形,即CD=CE=R,
∴ACCD=ABBF,即6R=10BF①,
BCCE=ABAF,即8R=BF②,
①②联立得,R=2.
∵直角三角形斜边为:10,
∴外接圆半径是:5.
故答案为:2,5.


科目:初中数学 来源: 题型:
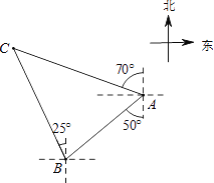
【题目】如图,国家规定休渔期间,我国渔政船在A处发现南偏西50°方向距A处20海里的点B处有一艘可疑船只,可疑船只正沿北偏西25°方向航行,我国渔政船立即沿北偏西70°方向前去拦截,经过1.5小时刚好在C处拦截住可疑船只,求该可疑船只航行的平均速度.
(结果精确到个位,参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
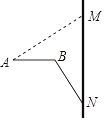
【题目】高铁给我们的出行带来了极大的方便.如图,“和谐号”高铁列车座椅后面的小桌板收起时,小桌板的支架的底端N与桌面顶端M的距离MN=75cm,且可以看作与地面垂直.展开小桌板使桌面保持水平,AB⊥MN,∠MAB=∠MNB=37°,且支架长BN与桌面宽AB的长度之和等于MN的长度.求小桌板桌面的宽度AB(结果精确到1cm,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
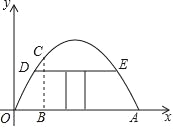
【题目】有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示,已知OA=8米,距离O点2米处的棚高BC为![]() 米.
米.
(1)求该抛物线的解析式;
(2)若借助横梁DE(DE∥OA)建一个门,要求门的高度为1.5米,求横梁DE的长度是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m﹣1)x+m2=0有两个实数根x1和x2.
(1)求实数m的取值范围;
(2)当x12﹣x22=0时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
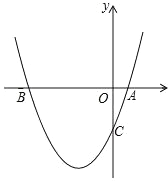
【题目】如图,已知二次函数 y=x2+bx+c 过点 A(1,0),C(0,﹣3)
(1)求此二次函数的解析式;
(2)求△ABC 的面积;
(3)在抛物线上存在一点 P 使△ABP 的面积为 10,请求出点 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表所示.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
下列说法:①抛物线与y轴的交点为(0,6); ②抛物线的对称轴在y轴的右侧;③抛物线一定经过点(3,0);④在对称轴左侧,y随x增大而减小.⑤不等式ax2+(b﹣3)x+c﹣6>0解集为﹣2<x<0.其中说法正确的有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
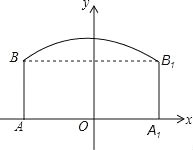
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m.
(1)按如图所示的直角坐标系,求表示该抛物线的函数表达式.
(2)一大型汽车装载某大型设备后,高为7m,宽为4m,如果该隧道内设双向行车道,那么这辆贷车能否安全通过?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com