
【题目】已知抛物线y=ax2+bx+c经过A(-4,3)、B(2,0)两点,当x=3和x=-3时,这条抛物线上对应点的纵坐标相等.经过点C(0,-2)的直线l与 x轴平行,O为坐标原点.

(1)求直线AB和这条抛物线的解析式;
(2)以A为圆心,AO为半径的圆记为⊙A,判断直线l与⊙A的位置关系,并说明理由;
(3)设直线AB上的点D的横坐标为-1,P(m,n)是抛物线y=ax2+bx+c上的动点,当△PDO的周长最小时,求四边形CODP的面积.
【答案】(1)y=![]() x2-1.
x2-1.
(2)直线l与⊙A相切
(3)![]()
【解析】(1)因为当x=3和x=-3时,这条抛物线上对应点的纵坐标相等,故b=0.
设直线AB的解析式为y=kx+b,把A(-4,3)、B(2,0)代入到y=ax2+bx+c,得
![]() 解得
解得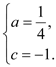
∴这条抛物线的解析式为y=![]() x2-1.
x2-1.
设直线AB的解析式为y=kx+b,把A(-4,3)、B(2,0)代入到y=kx+b,得
![]() 解得
解得
∴这条直线的解析式为y=-![]() x+1.
x+1.
(2)依题意,OA=![]() 即⊙A的半径为5.
即⊙A的半径为5.
而圆心到直线l的距离为3+2=5.
即圆心到直线l的距离=⊙A的半径,
∴直线l与⊙A相切.
(3)由题意,把x=-1代入y=-![]() x+1,得y=
x+1,得y=![]() ,即D(-1,
,即D(-1, ![]() ).
).
由(2)中点A到原点距离跟到直线y=-2的距离相等,且当点A成为抛物线上一个动点时,仍然具有这样的性质,于是过点D作DH⊥直线l于H,交抛物线于点P,此时易得DH是D点到l最短距离,点P坐标(-1,-![]() )此时四边形PDOC为梯形,面积为
)此时四边形PDOC为梯形,面积为![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=![]() 米时,有DC2=AE2+BC2.
米时,有DC2=AE2+BC2.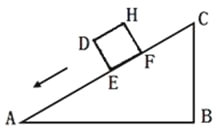
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中你能看出什么规律?

查看答案和解析>>
科目:初中数学 来源: 题型:
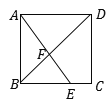
【题目】如图所示,在正方形ABCD中,点E是BC边上一点,且BE:EC=2:1,AE与BD交于点F,则△AFD与四边形DFEC的面积之比是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF. 
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 的值等于 .
的值等于 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com