
【题目】如图,△ABC是等边三角形,AB=6,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)证明:在运动过程中,点D是线段PQ的中点;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为宣传“扫黑除恶”专项行动,社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的90%,若设白边的宽为x米,则根据题意可列出方程( )

A. 90%×(2+x)(1+x)=2×1 B. 90%×(2+2x)(1+2x)=2×1
C. 90%×(2﹣2x)(1﹣2x)=2×1 D. (2+2x)(1+2x)=2×1×90%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是反比例函数y=![]() 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
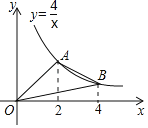
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)解方程:x4﹣5x2+4=0.
这是一个一元四次方程,根据该方程的特点,我们可以借助“换元法”将高次方程“降次”,进而解得未知数的值.
解:设 x2=y,那么 x4=y2,于是原方程可变为 y2﹣5y+4=0,解得 y1=1,y2=4. 当 y1=1 时,x2=1,x=±1;当 y2=4 时,x2=4,x=±2;
原方程有四个根:x1=1,x2=﹣1,x3=2,x4=﹣2.
(触类旁通)参照例题解方程:(x2+x)2﹣4(x2+x)﹣12=0;
(解决问题)已知实数 x,y 满足(2x+2y+3)(2x+2y﹣3)=27,求 x+y 的值;
(拓展迁移)分解因式:(x2+4x+3)(x2+4x+5)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 、
、![]() 为直线
为直线![]() 上的两动点,
上的两动点,![]() ,
,![]() ,
,![]() ;
;
(1)当点![]() 、
、![]() 重合,即
重合,即![]() 时(如图
时(如图![]() ),试求
),试求![]() .(用含
.(用含![]() ,
,![]() ,
,![]() 的代数式表示)
的代数式表示)
(2)请直接应用(1)的结论解决下面问题:当![]() 、
、![]() 不重合,即
不重合,即![]() ,
,
①如图![]() 这种情况时,试求
这种情况时,试求![]() .(用含
.(用含![]() ,
,![]() ,
,![]() ,
,![]() 的代数式表示)
的代数式表示)
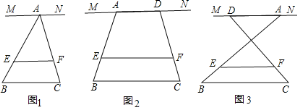
②如图![]() 这种情况时,试猜想
这种情况时,试猜想![]() 与
与![]() 、
、![]() 之间有何种数量关系?并证明你的猜想.
之间有何种数量关系?并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
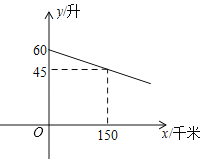
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写出自变量x的取值范围)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,求提示时汽车行驶的路程是多少千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com