
【题目】如图,已知抛物线y=ax2+4(a≠0)与x轴交于点A和点B(2,0),与y轴交于点C,点D是抛物线在第一象限的点.
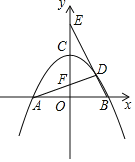
(1)当△ABD的面积为4时,
①求点D的坐标;
②联结OD,点M是抛物线上的点,且∠MDO=∠BOD,求点M的坐标;
(2)直线BD、AD分别与y轴交于点E、F,那么OE+OF的值是否变化,请说明理由.
【答案】(1)①![]() ;②
;②![]() ;(2)不变化,值为8,理由见解析
;(2)不变化,值为8,理由见解析
【解析】
(1)先将已知点B坐标代入解析式求出a,再根据△ABD的面积,求出D的纵坐标,将其代入抛物线求出D点坐标,根据∠MDO=∠BOD分两种情况讨论,并求出M坐标
(2)设出点D的坐标,利用平行线分线段成比例定理表示出OE、OF求和即可得出结论
(1)∵抛物线y=ax2+4(a≠0)与x轴交于点A和点B(2,0),
∴A(﹣2,0),4a+4=0,
∴a=﹣1,AB=4,
∴抛物线的解析式为y=﹣x2+4,
①设D(m,﹣m2+4),
∵△ABD的面积为4,
∴![]()
∴![]() ,
,
∵点D在第一象限,
∴![]() ,
,
∴![]() ,
,
②如图1,点M在OD上方时,
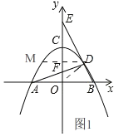
∵∠MDO=∠BOD,∴DM∥AB,
∴![]() ,当M在OD下方时,
,当M在OD下方时,
设DM交x轴于G,设G(n,0),
∴OG=n,
∵![]() ,
,
∴![]() ,
,
∵∠MDO=∠BOD,
∴OG=DG,
∴![]() ,
,
∴![]() ,
,
∴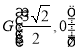 ,
,
∵![]() ,
,
∴直线DG的解析式为![]() ①,
①,
∵抛物线的解析式为y=﹣x2+4②,
联立①②得, ![]() ,此时交点刚好是D点,
,此时交点刚好是D点,
所以在OD下方不存在点M.
(2)OE+OF的值不发生变化,
理由:如图2,过点D作DH⊥AB于H,
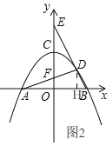
∴OF∥DH,
∴![]() ,
,
设D(b,﹣b2+4),
∴AH=b+2,DH=﹣b2+4,
∵OA=2,
∴![]() ,
,
∴![]() ,
,
同理:OE=2(2+b),
∴OE+OF=2(2﹣b)+2(2+b)=8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小张同学尝试运用课堂上学到的方法,自主研究函数y=![]() 的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
(1)函数y=![]() 自变量的取值范围是 ;
自变量的取值范围是 ;
(2)下表列出了y与x的几组对应值:
x | … | ﹣2 | ﹣ | m | ﹣ | ﹣ |
|
| 1 |
| 2 | … |
y | … |
|
| 1 |
| 4 | 4 |
| 1 |
|
| … |
表中m的值是 ;
(3)如图,在平面直角坐标系xOy中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图象;
(4)结合函数y=![]() 的图象,写出这个函数的性质: .(只需写一个)
的图象,写出这个函数的性质: .(只需写一个)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上海首条中运量公交线路71路已正式开通.该线路西起沪青平公路申昆路,东至延安东路中山东一路,全长17.5千米.71路车行驶于专设的公交车道,又配以专用的公交信号灯.经测试,早晚高峰时段71路车在专用车道内行驶的平均速度比在非专用车道每小时快6千米,因此单程可节省时间22.5分钟.求早晚高峰时段71路车在专用车道内行驶的平均车速.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与x轴、y轴分别交于A、B两点,设O为坐标原点.
与x轴、y轴分别交于A、B两点,设O为坐标原点.
(1)求∠ABO的正切值;
(2)如果点A向左平移12个单位到点C,直线l过点C且与直线![]() 平行,求直线l的解析式.
平行,求直线l的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,点E在边BC上,AE=BE,点M是AE的中点,联结CM,点G在线段CM上,作∠GDN=∠AEB交边BC于N.

(1)如图2,当点G和点M重合时,求证:四边形DMEN是菱形;
(2)如图1,当点G和点M、C不重合时,求证:DG=DN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,联结DE并延长至点F,使EF=AE,联结AF,CF,联结BE并延长交CF于点G.
(1)求证:BC=DF;
(2)若BD=2DC,求证:GF=2EG;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
(1)求点A,点B的坐标;
(2)P为第二象限抛物线上的一个动点,求△ACP面积的最大值.
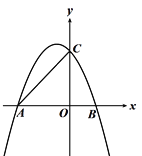
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:两个图形![]() 和
和![]() ,在
,在![]() 上的任意一点
上的任意一点![]() 引出两条垂直的射线与
引出两条垂直的射线与![]() 相交于点
相交于点![]() 、
、![]() ,如果
,如果![]() ,我们就称
,我们就称![]() 、
、![]() 为点
为点![]() 的垂等点,
的垂等点,![]() 、
、![]() 为点
为点![]() 的垂等线段,点
的垂等线段,点![]() 为垂等射点.
为垂等射点.
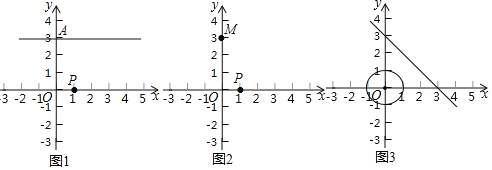
(1)如图1,在平面直角坐标系![]() 中,点
中,点![]() 为
为![]() 轴上的垂等射点,过
轴上的垂等射点,过![]() 作
作![]() 轴的平行线
轴的平行线![]() ,则直线
,则直线![]() 上的
上的![]() 为点
为点![]() 的垂等点的是_______;
的垂等点的是_______;
(2)如果一次函数图象过![]() ,点
,点![]() 为垂等射点
为垂等射点![]() 的一个垂等点且另一个垂等点
的一个垂等点且另一个垂等点![]() 也在此一次函数图象上,在图2中画出示意图并写出一次函数表达式;
也在此一次函数图象上,在图2中画出示意图并写出一次函数表达式;
(3)如图3,以点![]() 为圆心,1为半径作
为圆心,1为半径作![]() ,垂等射点
,垂等射点![]() 在
在![]() 上,垂等点在经过(3,0),(0,3)的直线上,如果关于点
上,垂等点在经过(3,0),(0,3)的直线上,如果关于点![]() 的垂等线段始终存在,求垂等线段
的垂等线段始终存在,求垂等线段![]() 长的取值范围(画出图形直接写出答案即可).
长的取值范围(画出图形直接写出答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选择:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其他),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):

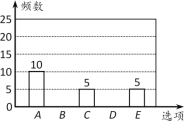
根据以上信息解答下列问题:
⑴ 这次被调查的学生有多少人?
⑵ 表中m的值为 ,并补全条形统计图;
⑶若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com