
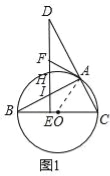
【题目】如图1,BC是⊙O的直径,点A在⊙O上,点D在CA的延长线上,DE⊥BC,垂足为点E,DE与⊙O相交于点H,与AB相交于点l,过点A作⊙O的切线AF,与DE相交于点F.
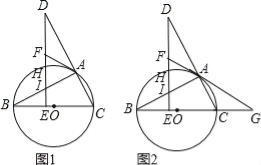
(1)求证:∠DAF=∠ABO;
(2)当AB=AD时,求证:BC=2AF;
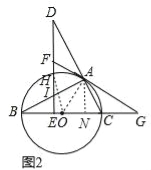
(3)如图2,在(2)的条件下,延长FA,BC相交于点G,若tan∠DAF=![]() ,EH=2
,EH=2![]() ,求线段CG的长.
,求线段CG的长.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
试题分析:(1)连接AO,如图1,由OA=OB可得∠OAB=∠OBA,要证∠DAF=∠ABO,只需证∠DAF=∠BAO,只需证∠FAO=∠DAB=90°即可;
(2)由于BC=2OA,要证BC=2AF,只需证OA=AF,只需证△AFD≌△AOB即可;
(3)过点A作AN⊥BC于N,连接OH,OA,如图2,易得BE=2IE,DE=2EC,DI=2AF=BC,从而可得EC=3IE=![]() BE.设BE=2x,则有EC=3x,BC=5x,HO=BO=
BE.设BE=2x,则有EC=3x,BC=5x,HO=BO=![]() ,EO=
,EO=![]() .在Rt△HEO中运用勾股定理可求出x.利用三角函数可得BN=2AN=4NC,则有BC=5NC=10,从而可求出NC、ON,易证△AON∽△GOA,根据相似三角形的性质可求出OG,从而可求出CG.
.在Rt△HEO中运用勾股定理可求出x.利用三角函数可得BN=2AN=4NC,则有BC=5NC=10,从而可求出NC、ON,易证△AON∽△GOA,根据相似三角形的性质可求出OG,从而可求出CG.
试题解析:(1)连接AO,如图1.
∵AF与⊙O相切于点A,
∴OA⊥AF,即∠FAO=90°.
∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠DAB=90°,
∴∠FAO=∠DAB=90°,
∴∠DAF=∠BAO.
∵OA=OB,
∴∠OAB=∠OBA,
∴∠DAF=∠ABO;
(2)∵DE⊥BC,∴∠DEB=90°,
∴∠DIB=90°+∠ABO.
∵∠DIB=90°+∠D,
∴∠D=∠ABO.
在△AFD和△AOB中,
 ,
,
∴△AFD≌△AOB,
∴AF=AO,
∴BC=2OA=2AF;
(3)过点A作AN⊥BC于N,连接OH,OA,如图2.
∵∠D=∠B=∠BAO=∠DAF,tan∠DAF=![]() ,
,
∴tanB=![]() ,tanD=
,tanD=![]() ,
,
∴BE=2IE,DE=2EC.
又∵∠DIA+∠D=∠DAF+∠FAI=90°,
∴∠FIA=∠FAI,
∴FI=FA,
∴DI=2AF=BC,
∴DE﹣IE=BE+EC,
∴2EC﹣IE=2IE+EC,
∴EC=3IE=![]() BE.
BE.
设BE=2x,则有EC=3x,BC=5x,HO=BO=![]() ,EO=
,EO=![]() .
.
在Rt△HEO中,根据勾股定理可得
(![]() )2+(2
)2+(2![]() )2=(
)2=(![]() )2,
)2,
解得x=2(舍负).
∵AN⊥BC,∠BAC=90°,
∴∠NAC=∠ABC,
∴tan∠NAC=![]() ,tan∠ABC=
,tan∠ABC=![]() ,
,
∴BN=2AN=4NC,
∴BC=5NC=10,
∴NC=2,ON=5﹣2=3.
∵∠AON=∠GOA,∠ANO=∠OAG=90°,
∴△AON∽△GOA,
∴![]() ,
,
∴![]() ,
,
∴OG=![]() ,
,
∴CG=OG﹣OC=![]() .
.


科目:初中数学 来源: 题型:
【题目】为了增强青少年的防毒拒毒意识,学校举办了一次“禁毒教育”演讲比赛,其中某位选手的演讲内容、语言表达、演讲技巧这三项得分分别为90分,80分,85分,若依次按50%,30%,20%的比例确定成绩,则该选手的最后得分是__________分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一测量爱好者,在海边测量位于正东方向的小岛高度AC,如图所示,他先在点B测得山顶点A的仰角为30°,然后向正东方向前行62米,到达D点,在测得山顶点A的仰角为60°(B、C、D三点在同一水平面上,且测量仪的高度忽略不计).求小岛高度AC(结果精确的1米,参考数值:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
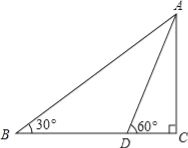
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭历史悠久,因盛产湘莲,被誉为“莲城”.李红买了8个莲蓬,付50元,找回38元,设每个莲蓬的价格为x元,根据题意,列出方程为__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下调查中,适宜全面调查的是( )
A. 调查某批次汽车的抗撞击能力B. 调查某班学生的身高情况
C. 调查春节联欢晚会的收视率D. 调查济宁市居民日平均用水量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知□ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
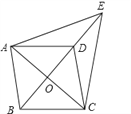
(1)四边形ABCD是菱形吗?请说明理由;
(2)若∠AED=2∠EAD,试说明四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在五张正面分别写有数字﹣2,﹣1,0,1,2的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀.
(1)从中任意抽取一张卡片,则所抽卡片上数字的绝对值不大于1的概率是 ;
(2)先从中任意抽取一张卡片,以其正面数字作为a的值,然后再从剩余的卡片随机抽一张,以其正面的数字作为b的值,请用列表法或画树状图法,求点Q(a,b)在第二象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com