
分析 根据通话时间与收费标准,可得函数解析式,根据函数值,可得相应自变量的值.
解答 解:当x≤3时,y=2.4,
当x>3时,y=x-0.6,
综上所述:$\left\{\begin{array}{l}{2.4(x≤3)}\\{x-0.6(x>3)}\end{array}\right.$y=$\left\{\begin{array}{l}{2.4(x≤3)}\\{x+0.6(x>3)}\end{array}\right.$;
当y=10时,x-0.6=10,
解得x=10.6.
答:有10元钱时,打一次电话最多可以通话10.6分钟.
点评 本题考查了分段函数,分类讨论是解题关键,利用通话时间与收费标准得出函数关系式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
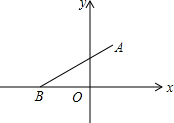 如图,在平面直角坐标系中,点A的坐标为(1,$\sqrt{3}$),点B在x轴的负半轴上,∠ABO=30°.
如图,在平面直角坐标系中,点A的坐标为(1,$\sqrt{3}$),点B在x轴的负半轴上,∠ABO=30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $2\sqrt{5}$ | B. | $2\sqrt{5}$或$4\sqrt{5}$ | C. | $4\sqrt{5}$ | D. | $2\sqrt{5}$或6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
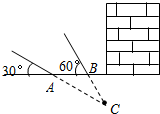 北京时间2015年04月25日14时11分,尼泊尔发生强烈地震,震级8.1级左右.在地震抢救中,某探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距4米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(参考数据:$\sqrt{3}$≈1.732,结果保留一位小数).
北京时间2015年04月25日14时11分,尼泊尔发生强烈地震,震级8.1级左右.在地震抢救中,某探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距4米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(参考数据:$\sqrt{3}$≈1.732,结果保留一位小数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com