
分析 (1)由∠FAE=16°,∠FAD=31°可知∠EAD=15°,根据AF∥BE可知∠AED=∠FAE=16°,∠ADB=∠FAD=31°,设AB=x,则在Rt△AEB中,EB=$\frac{AB}{tan16°}$,在Rt△ADB中,BD=$\frac{AB}{tan31°}$,根据BE-BD=4列出方程,解方程求出x的值即可;
(2)先由BD=$\frac{AB}{tan31°}$求出BD,再根据CD=BD-BC求出CD,与2米进行比较即可.
解答 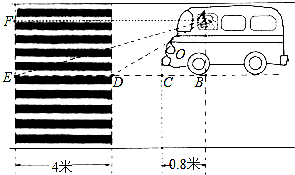 解:(1)∵∠FAE=16°,∠FAD=31°,
解:(1)∵∠FAE=16°,∠FAD=31°,
∴∠EAD=15°,
∵AF∥BE,
∴∠AED=∠FAE=16°,∠ADB=∠FAD=31°,
设AB=x,
则在Rt△AEB中,
EB=$\frac{AB}{tan16°}$=$\frac{x}{tan16°}$,
在Rt△ADB中,BD=$\frac{AB}{tan31°}$=$\frac{x}{tan31°}$,
∵BE-BD=ED=4,
∴$\frac{x}{tan16°}$-$\frac{x}{tan31°}$=4,
即($\frac{1}{0.28}$-$\frac{1}{0.60}$)x=4,
解得x≈2.10,即AB≈2.10米,
答:旅游车高至少2.10米;
(2)∵AB≈2.10米,
∴BD=$\frac{AB}{tan31°}$≈$\frac{2.10}{0.60}$=3.5,
∴CD=BD-BC≈3.5-0.8=2.7>2,故符合标准.
答:该旅游车停车符合上述安全标准.
点评 本题考查的是解直角三角形的应用,根据题意找出符合条件的直角三角形,利用直角三角形的性质进行解答是解答本题的关键.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
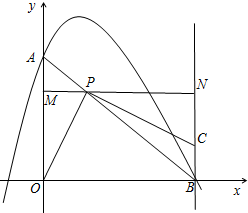 如图,抛物线y=-2x2+x+1交y轴于点A,交x轴正半轴于点B.P为线段AB上一动点,作直线PC⊥PO,交过点B垂直于x轴的直线于点C.过P点作直线MN平行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.
如图,抛物线y=-2x2+x+1交y轴于点A,交x轴正半轴于点B.P为线段AB上一动点,作直线PC⊥PO,交过点B垂直于x轴的直线于点C.过P点作直线MN平行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
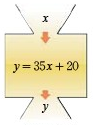 地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间的关系可以近似地用关系式y=35x+20来表示.当x的值是5时,y=195.
地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间的关系可以近似地用关系式y=35x+20来表示.当x的值是5时,y=195.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com