
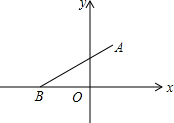
 ��ͼ����ƽ��ֱ������ϵ�У���A������Ϊ��1��$\sqrt{3}$������B��x��ĸ������ϣ���ABO=30�㣮
��ͼ����ƽ��ֱ������ϵ�У���A������Ϊ��1��$\sqrt{3}$������B��x��ĸ������ϣ���ABO=30�㣮���� ��1������A��AF��x���ڵ�F������ֱ�ǡ�ABF��ͨ�����ֱ���������õ�B�����꣬��ú���ͼ����B��ԭ�㣬����������ʽ����������ʽ���ɣ�
��2������A��AF��ֱ��x���ڵ�F�������ߵĶԳ���x=-1��x���ڵ�E������Cλ�ڶԳ������߶�AB�Ľ���ʱ��AC+OC��ֵ��С���������������Ρ�BCE�ס�BAF����������CE�ij��ȣ����õ�C�����ꣻ
��3����ͼ2������AO����p��x��y��������ֱ��AB�Ľ���ʽ���ɸý���ʽ�����������߶εij��ȣ������֪����������ͼ�������ı�����ϵ�������ε������ʽ�õ�����x�ķ��̣�ͨ���ⷽ����õ�P�����꼴�ɣ�
��� 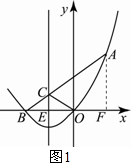 �⣺��1������A��AF��x���ڵ�F��
�⣺��1������A��AF��x���ڵ�F��
�ߡ�ABO=30�㣬A������Ϊ��1��$\sqrt{3}$����
��BF=3��
��OF=1��
��BO=2��
��B��-2��0����
�������ߵĽ���ʽΪy=ax��x+2���������A��1��$\sqrt{3}$������$a=\frac{{\sqrt{3}}}{3}$��
��$y=\frac{{\sqrt{3}}}{3}{x^2}+\frac{{2\sqrt{3}}}{3}x$��
��2�����ڵ�C��
����A��AF��ֱ��x���ڵ�F�������ߵĶԳ���x=-1��x���ڵ�E��
����Cλ�ڶԳ������߶�AB�Ľ���ʱ��AC+OC��ֵ��С��
�ߡ�BCE�ס�BAF��
��$\frac{BE}{BF}=\frac{CE}{AF}$��
��$CE=\frac{BE•AF}{BF}=\frac{{\sqrt{3}}}{3}$
��C��-1��$\frac{{\sqrt{3}}}{3}$����
��3�����ڣ�
��ͼ2������AO��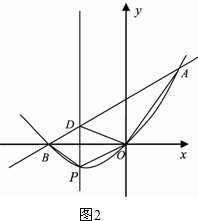 ��p��x��y����ֱ��ABΪy=kx+b��k��0������$\left\{\begin{array}{l}k+b=\sqrt{3}\\-2k+b=0.\end{array}\right.���\left\{\begin{array}{l}k=\frac{{\sqrt{3}}}{3}\\ b=\frac{{2\sqrt{3}}}{3}\end{array}\right.$��
��p��x��y����ֱ��ABΪy=kx+b��k��0������$\left\{\begin{array}{l}k+b=\sqrt{3}\\-2k+b=0.\end{array}\right.���\left\{\begin{array}{l}k=\frac{{\sqrt{3}}}{3}\\ b=\frac{{2\sqrt{3}}}{3}\end{array}\right.$��
��ֱ��ABΪ$y=\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}$��S�ı���BPOD=S��BPO+S��BOD=$\frac{1}{2}$|OB||yP|+$\frac{1}{2}$|OB||yD|=|yP|+|yD|
=$-\frac{{\sqrt{3}}}{3}{x^2}-\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}$��
��S��AOD=S��AOB-S��BOD=$\sqrt{3}$-$\frac{1}{2}$��2��|$\frac{{\sqrt{3}}}{3}$x+$\frac{{2\sqrt{3}}}{3}$|=-$\frac{{\sqrt{3}}}{3}$x+$\frac{{\sqrt{3}}}{3}$��
��$\frac{{{S_{��AOD}}}}{{{S_{��BPOD}}}}$=${\frac{{-\frac{{\sqrt{3}}}{3}x+\frac{{\sqrt{3}}}{3}}}{{-\frac{{\sqrt{3}}}{3}{x^2}-\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}}}^{\;}}$=$\frac{2}{3}$��
��x1=-$\frac{1}{2}$��x2=1����ȥ����
��p��-$\frac{1}{2}$��-$\frac{{\sqrt{3}}}{4}$����
�֡�S��BOD=$\frac{{\sqrt{3}}}{3}$x+$\frac{{2\sqrt{3}}}{3}$��
��$\frac{{{S_{��BOD}}}}{{{S_{��BPOD}}}}$=$\frac{{\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}}}{{-\frac{{\sqrt{3}}}{3}{x^2}-\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}}}$=$\frac{2}{3}$��
��������
2x2+5x+2=0��
��x1=-$\frac{1}{2}$��x2=-2��
P��-2��0�������������⣮
����ڣ���P�����ǣ�-$\frac{1}{2}$��-$\frac{{\sqrt{3}}}{4}$����
���� ���⿼���˶��κ����ۺ��⣮��������У��漰���˴���ϵ������һ�κ��������κ�������ʽ�����������ε��ж������ʣ������ε������ʽ��֪ʶ�㣬�ѶȽϴ��ۺ��ԱȽ�ǿ��


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 100�� | B�� | 120�� | C�� | 80�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3 | B�� | 3 | C�� | -3 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
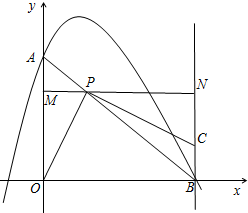 ��ͼ��������y=-2x2+x+1��y���ڵ�A����x���������ڵ�B��PΪ�߶�AB��һ���㣬��ֱ��PC��PO��������B��ֱ��x���ֱ���ڵ�C����P����ֱ��MNƽ����x�ᣬ��y���ڵ�M��������B��ֱ��x���ֱ���ڵ�N��
��ͼ��������y=-2x2+x+1��y���ڵ�A����x���������ڵ�B��PΪ�߶�AB��һ���㣬��ֱ��PC��PO��������B��ֱ��x���ֱ���ڵ�C����P����ֱ��MNƽ����x�ᣬ��y���ڵ�M��������B��ֱ��x���ֱ���ڵ�N���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com