
【题目】如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.
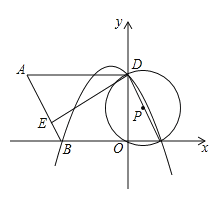
(1)求抛物线的解析式;
(2)求证:ED是⊙P的切线;
(3)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
【答案】(1)y=-![]() x2-
x2-![]() x+2
x+2![]() ;(2)证明见解析;(3)存在,点N的坐标为(-5,
;(2)证明见解析;(3)存在,点N的坐标为(-5,![]() )、(3,
)、(3,![]() )、(-3,-
)、(-3,-![]() ).
).
【解析】
试题分析:(1)先确定B(-4,0),再在Rt△OCD中利用∠OCD的正切求出OD=2![]() ,D(0,2
,D(0,2![]() ),然后利用交点式求抛物线的解析式;
),然后利用交点式求抛物线的解析式;
(2)先计算出CD=2OC=4,再根据平行四边形的性质得AB=CD=4,AB∥CD,∠A=∠BCD=60°,AD=BC=6,则由AE=3BE得到AE=3,接着计算![]()
,加上∠DAE=∠DCB,则可判定△AED∽△COD,得到∠ADE=∠CDO,而∠ADE+∠ODE=90°则∠CDO+∠ODE=90°,再利用圆周角定理得到CD为⊙P的直径,于是根据切线的判定定理得到ED是⊙P的切线
(3)利用配方得到y=-![]() (x+1)2+
(x+1)2+![]() ,则M(-1,
,则M(-1,![]() ),且B(-4,0),D(0,2
),且B(-4,0),D(0,2![]() ),根据平行四边形的性质和点平移的规律,利用分类讨论的方法确定N点坐标.
),根据平行四边形的性质和点平移的规律,利用分类讨论的方法确定N点坐标.
试题解析:(1)∵C(2,0),BC=6,
∴B(-4,0),
在Rt△OCD中,∵tan∠OCD=![]() ,
,
∴OD=2tan60°=2![]() ,
,
∴D(0,2![]() ),
),
设抛物线的解析式为y=a(x+4)(x-2),
把D(0,2![]() )代入得a4(-2)=2
)代入得a4(-2)=2![]() ,解得a=-
,解得a=-![]() ,
,
∴抛物线的解析式为y=-![]() (x+4)(x-2)=-
(x+4)(x-2)=-![]() x2-
x2-![]() x+2
x+2![]() ;
;
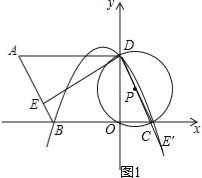
(2)在Rt△OCD中,CD=2OC=4,
∵四边形ABCD为平行四边形,
∴AB=CD=4,AB∥CD,∠A=∠BCD=60°,AD=BC=6,
∵AE=3BE,
∴AE=3,
∴![]() ,
,![]() ,
,
∴![]() ,
,
而∠DAE=∠DCB,
∴△AED∽△COD,
∴∠ADE=∠CDO,
而∠ADE+∠ODE=90°
∴∠CDO+∠ODE=90°,
∴CD⊥DE,
∵∠DOC=90°,
∴CD为⊙P的直径,
∴ED是⊙P的切线;
(3)存在.
∵y=-![]() x2-
x2-![]() x+2
x+2![]() =-
=-![]() (x+1)2+
(x+1)2+![]()
∴M(-1,![]() ),
),
而B(-4,0),D(0,2![]() ),
),
如图2,
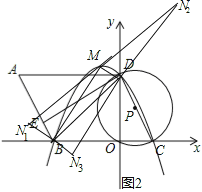
当BM为平行四边形BDMN的对角线时,点D向左平移4个单位,再向下平移2![]() 个单位得到点B,则点M(-1,
个单位得到点B,则点M(-1,![]() )向左平移4个单位,再向下平移2
)向左平移4个单位,再向下平移2![]() 个单位得到点N1(-5,
个单位得到点N1(-5,![]() );
);
当DM为平行四边形BDMN的对角线时,点B向右平移3个单位,再向上平移![]() 个单位得到点M,则点D(0,2
个单位得到点M,则点D(0,2![]() )向右平移3个单位,再向上平移
)向右平移3个单位,再向上平移![]() 个单位得到点N2(3,
个单位得到点N2(3,![]() );
);
当BD为平行四边形BDMN的对角线时,点M向左平移3个单位,再向下平移![]() 个单位得到点B,则点D(0,2
个单位得到点B,则点D(0,2![]() )向右平移3个单位,再向下平移
)向右平移3个单位,再向下平移![]() 个单位得到点N3(-3,-
个单位得到点N3(-3,-![]() ),
),
综上所述,点N的坐标为(-5,![]() )、(3,
)、(3,![]() )、(-3,-
)、(-3,-![]() ).
).


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2(a>0)过A(﹣2,y1)、B(1,y2)两点,则下列关系式一定正确的是( )
A. y1>0>y2 B. y2>0>y1 C. y1>y2>0 D. y2>y1>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在烟台市举办的“读好书、讲礼仪”活动中,东华学校积极行动,各班图书角的新书、好书不断增多,除学校购买外,还有师生捐献的图书,下面是七年级(1)班全体同学捐献图书的情况统计图:
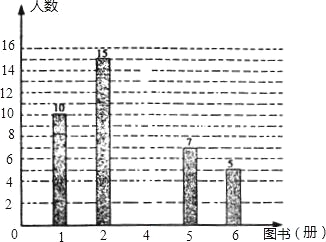
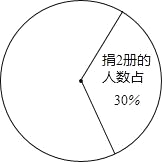
请你根据以上统计图中的信息,解答下列问题:
(1)该班有学生多少人?
(2)补全条形统计图;
(3)七(1)班全体同学所卷图书的中位数和众数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学想利用木条为七年级数学组制作一个三角形的工具,那么下列哪组数据的三根木条的长度能符合他的要求?( )
A、4,2,2 B、3,6,6 C、2,3,6 D、7,13,6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定7名同学参加决赛,他们的决赛成绩各不相同,其中李华已经知道自己的成绩,但能否进前四名,他还必须清楚这七名同学成绩的( )
A. 众数 B. 平均数 C. 中位数 D. 方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com