
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,
①△ADC是 三角形;
②设△BDC的面积为![]() ,△AEC的面积为
,△AEC的面积为![]() ,则
,则![]() 与
与![]() 的数量关系是 .
的数量关系是 .
(2)猜想论证:当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中![]() 与
与![]() 的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究:如图4,已知∠ABC=60°,点D是角平分线上一点,且BD=CD=4,DE∥AB交BC于点E.若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.


【答案】(1)①等边;②S1=S2;(2)![]() ,理由见解析;(3)BF=
,理由见解析;(3)BF=![]() 或BF=
或BF=![]()
【解析】试题分析:(1)①根据AC=CD,∠BAC=60°,即可判定△ACD是等边三角形;
②根据DE∥AC,可得S△ACE=S△ACD,根据点D是AB的中点,可得S△BDC=S△ACD,进而得到△BDC的面积和△AEC的面积相等,即S1=S2;
(2)先判定△ACN≌△DCM(AAS),得出AN=DM,再根据等底等高的三角形的面积相等可得,△BDC的面积和△AEC的面积相等,即S1=S2;
(3)先作EG⊥BD于G,延长CD交AB于H,根据等底等高的三角形的面积相等,可得EG=HF=![]() ,最后根据线段的和差关系,即可求得BF的长.
,最后根据线段的和差关系,即可求得BF的长.
试题解析:(1)①∵△DEC绕点C旋转,点D恰好落在AB边上,
∴AC=CD,
∵∠BAC=90°-∠B=90°-30°=60°,
∴△ACD是等边三角形,②∵△ACD是等边三角形,
∴∠ACD=60°,
又∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE,
∴DE∥AC,
∴根据同底等高的三角形面积相等,可得S△ACE=S△ACD,
∵∠B=30°,∠ACB=90°,
∴Rt△ABC中,AC=![]() AB=AD,
AB=AD,
∴点D是AB的中点,
∴S△BDC=S△ACD,
∴△BDC的面积和△AEC的面积相等,即S1=S2,
(2)如图,
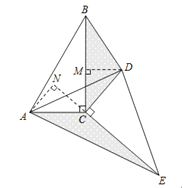
∵△DEC是由△ABC绕点C旋转得到,
∴BC=CE,AC=CD
![]() ,
,
![]() ,……… 6分
,……… 6分
在△ACN和△DCM中,
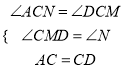 ,
,
![]() ,
,
∴AN=DM
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即![]()
(3)BF=![]() 或BF=
或BF=![]() .
.
理由:如图,作EG⊥BD于G,延长CD交AB于H,
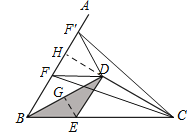
∵BD平分∠ABC,∠ABC=60°,DE∥AB,
∴∠ABD=∠DBE=∠BDE=30°,
∴ED=EB,
∴BG=![]() BD=2,
BD=2,
∴Rt△BEG中,GE=![]() ,
,
∵DB=DC=4,
∴∠BCD=∠DBC=30°,
∴∠ABC=60°,
∴∠CHB=90°,即CH⊥AB,
∵S△DCF=S△BDE,DB=DC,
∴△CDF中CD边上的高等于![]() ,
,
当点F在HB上时,HF=![]() ,
,
又∵Rt△BDH中,DH=![]() BD=2,∠DBH=30°,
BD=2,∠DBH=30°,
∴BH=![]() DH=2
DH=2![]() ,
,
∴BF=BH-FH=2![]() -
-![]() =
=![]() ;
;
当点F'在BH延长线上时,同理可得HF'=![]() ,
,
∴BF'=BH+F'H=2![]() +
+![]() =
=![]() .
.
综上所述,BF的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知AC是矩形ABCD的对角线,AC的垂直平分线EF分别交BC、AD于点E和F,EF交AC于点O.
(1)求证:四边形AECF是菱形;(2)若AB=6,AD=8,求四边形AECF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,点A0位于坐 标原点,点A1,A2,A3,…,A2017在
的图象如图所示,点A0位于坐 标原点,点A1,A2,A3,…,A2017在![]() 轴的正半轴上,点B1, B2, B3,…,B2017在二次函数
轴的正半轴上,点B1, B2, B3,…,B2017在二次函数![]() 位于第一象限的图象上,△A0B1A1,△A1B2A2,△A2B3A3,…,△A2016B2017A2017都为等边三角形,则等边△A2016B2017A2017的高为_____.
位于第一象限的图象上,△A0B1A1,△A1B2A2,△A2B3A3,…,△A2016B2017A2017都为等边三角形,则等边△A2016B2017A2017的高为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
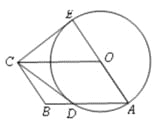
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长 AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若平行四边形OABC的两边长是方程![]() 的两根,求平行四边形OABC的面积.
的两根,求平行四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF为直角三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,E是AB上一点,线段DE与菱形对角线AC交于点F,点O是AC的中点,EO的延长线交边DC于点G
(1)求证:∠AED=∠FBC;
(2)求证:四边形DEBG是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】9岁的小芳身高1.36米,她的表姐明年想报考北京的大学.表姐的父母打算今年暑假带着小芳及其表姐先去北京旅游一趟,对北京有所了解.他们四人7月31日下午从无锡出发,1日到4日在北京旅游,8月5日上午返回无锡.
无锡与北京之间的火车票和飞机票价如下:火车 (高铁二等座) 全票524元,身高1.1~1.5米的儿童享受半价票;飞机 (普通舱) 全票1240元,已满2周岁未满12周岁的儿童享受半价票.他们往北京的开支预计如下:
住宿费 (2人一间的标准间) | 伙食费 | 市内交通费 | 旅游景点门票费 (身高超过1.2米全票) |
每间每天x元 | 每人每天100元 | 每人每天y元 | 每人每天120元 |
假设他们四人在北京的住宿费刚好等于上表所示其他三项费用之和,7月31日和8月5日合计按一天计算,不参观景点,但产生住宿、伙食、市内交通三项费用.
(1)他们往返都坐火车,结算下来本次旅游总共开支了13668元,求x,y的值;
(2)若去时坐火车,回来坐飞机,且飞机成人票打五五折,其他开支不变,他们准备了14000元,是否够用? 如果不够,他们准备不再增加开支,而是压缩住宿的费用,请问他们预定的标准间房价每天不能超过多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.

(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com