
����Ŀ���������������ͼ ����������DEF����������ֱ�������ABC�ı�AB��BC��AC�ϣ������dzơ�DEF������ABC���ڽ��������Σ�
��1����֤����ADF�ա�BED��
��������������ֱ�ߺ�Բ�����������ε��ڽ���������(������ͼ�ۼ�����д����)��
��2����ͼ ��������ABC�ı߳�Ϊa��������ABC���ڽ�����DEF��ʹ��DEF�ı߳���̣���˵�����ɣ�
��3����ͼ����������ABC���ڽ�����DEF��ʹFD��AB��
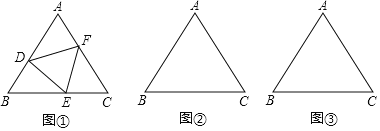
���𰸡���1��֤������������2����ͼ�����������ɼ���������3����ͼ��������
��������
���������
��1���ɵȱ������ε�����DF=DE����A=��B=60�������������ڽǺͿɵá�ADF=��BED������֤��ADF�ա�BED��
��������
��2����S��DEF=![]() ����֪��S��DEF��Сʱ��DF�ij���С����BD=x����AD=BE=a-x���ɵ�S��BED=
����֪��S��DEF��Сʱ��DF�ij���С����BD=x����AD=BE=a-x���ɵ�S��BED=![]() BEDG= =-
BEDG= =-![]() ��x-
��x-![]() ��2+
��2+![]() a2��Ȼ����ݶ��κ�����������⼴�ɣ�
a2��Ȼ����ݶ��κ�����������⼴�ɣ�
��3����AB��AC�Ĵ�ֱƽ���߽���ΪO������AO����AO�Ĵ�ֱƽ���߽�AB��D����OΪԲ�ģ�ODΪ�뾶��Բ����AC�ڵ�F����BC�ڵ�E��������⣮
֤����1���ߡ�ABC����DEF�����������Σ�
���A=��B=60������EDF=60����DF=ED��
�ߡ�ADF+��EDF=��B+��BED��
���ADF=��BED����DF=DE����A=��B=60����
���ADF�ա�BED��
��������
��2����ͼ��ʾ��
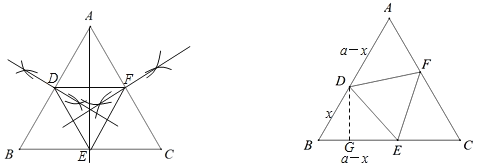
���ɣ��ɣ�1��֪��ADF�ա�BED��
ͬ����֤��BED�ա�CEF��
����ADF�ա�BED�ա�CEF��
����D��DG��BE����BD=x����AD=BE=a��x��DG=sinB��BD![]() x��
x��
S��BED![]() BEDG
BEDG![]() (a��x)��
(a��x)��![]() x
x![]() (x
(x![]() )2
)2![]() a2��
a2��
����BD![]() ������D��E��F�Ǹ����е�ʱ��S��BED�����ֵ
������D��E��F�Ǹ����е�ʱ��S��BED�����ֵ![]() a2��
a2��
��ʱ��ADF����CEF�������Ϊ���![]() a2(����ABC���ķ�֮һ)��
a2(����ABC���ķ�֮һ)��
���ڽ�����DEF�������С�����߳���̣�
��3����ͼ��ʾ��
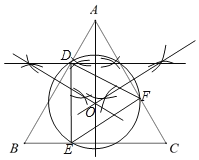


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪������y��x2��2ax+b�Ķ�����x���ϣ�P��x1��m����Q��x2��m����x1��x2���Ǵ��������ϵ����㣮
��1����a��1��
�ٵ�m��bʱ����x1��x2��ֵ��
�ڽ���������y��ƽ�ƣ�ʹ������x������������ľ���Ϊ4������������һ�仯���̣�
��2��������ʵ��c��ʹ��x1��c��1����x2��c+7��������m��ȡֵ��Χ��_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���Rt��ABC�У���BAC��90����BC��2����P����ABC�ڲ���һ�����㣬�������PBC����PCA�����߶�AP������СֵΪ��������
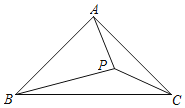
A.0.5B.![]() ��1C.2��
��1C.2��![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɽ��ʡÿ����������Էֳɱؿ���Ŀ��ѡ����Ŀ�����֣�����ѡ����Ŀ�Ǵ�һ������������ʵ������λ��ǰ�������������ĸ���Ŀ��ѡȡһ�������������һ�Ժ������Ҷ���2020��μ��п���ʵ�����������������������dz�ǿ����������ѡ�����ĸ���Ŀ�У�����һ������ѡʵ����
��1��������ѡ����Ŀ�У�ѡ����λ��ǰ���ĸ����� ��
��2������������ѡȡͬһ��ѡ����Ŀ�ĸ����Ƕ��٣� (�ڻ���״ͼ���б�ʱ����һ��������"�á�![]() ����ʾ������λ��ǰ�����á�
����ʾ������λ��ǰ�����á�![]() "��ʾ���������������á�
"��ʾ���������������á�![]() ����ʾ������ʵ�����á�
����ʾ������ʵ�����á�![]() ����ʾ)
����ʾ)
��3��ͨ������ʡij��2020��μ��п���ѧ������������飬���ָ���ѡ����λ��ǰ������ѧ����Ƶ���ȶ���![]() ���ң���֪������
���ң���֪������![]() �˲μ�2020���п����������ɴ˹��Ƹ�����
�˲μ�2020���п����������ɴ˹��Ƹ�����![]() ��ѧ����ѡ����λ��ǰ������������
��ѧ����ѡ����λ��ǰ������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ס�����������ͼ��ʾ������������ת��(�ֱ����ȷֺ��ĵȷ�)����Ϸ�������ǣ�ת������ת�̸�1�Σ�������ת��ֹͣת����ָ�������������������֮��Ϊ���������ʤ�������һ�ʤ�����ʤ�ĸ��ʣ�
��2����һ�������Ĵ��з������ɫ�ⶼ��ͬ��1�������n�������Ⱥ������������2�������������г��ֺ���ĸ����루1���м�ʤ�ĸ�����ͬ����n= ��
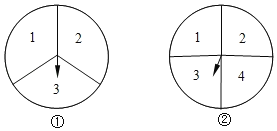
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��![]() �ڽ��ڡ�O����C������CP��BA���ӳ��߽��ڵ�P��
�ڽ��ڡ�O����C������CP��BA���ӳ��߽��ڵ�P��![]() ��
��

��1����֤��CP�ǡ�O�����ߣ�
��2����![]() ,
,![]() ����AB�ij���
����AB�ij���
��3����ͼ2��D��BC���е㣬PD��AC���ڵ�E,��֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������![]() �Ķ���Ϊ
�Ķ���Ϊ![]() �������������ϵ�����
�������������ϵ�����![]() ��
��![]() ��ֱ�߽������ߵĶԳ����ڵ�
��ֱ�߽������ߵĶԳ����ڵ�![]() ��
��
��1���������ߵĽ���ʽ��ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2������������![]() ����֮��IJ��֣�������
����֮��IJ��֣�������![]() ���㣩���Ƿ���ڵ�
���㣩���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �������ڣ������
�������ڣ������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
��3������![]() ���������ϣ���
���������ϣ���![]() ��
��![]() ���ϣ����Ե�
���ϣ����Ե�![]() Ϊ������ı�����ƽ���ı���ʱ��ֱ��д�����������ĵ�
Ϊ������ı�����ƽ���ı���ʱ��ֱ��д�����������ĵ�![]() �����꣮
�����꣮
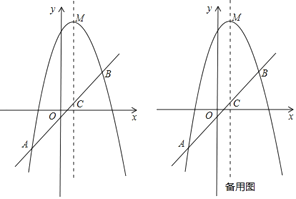
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǰ�����֮��Ϊ�����������γ�Ϊ���������Σ����У���������ȳ�Ϊ���ȣ��������߽����������εĵף�
��1����ͼ1����ABC����ACΪ�ı��������Σ�����Ϊ3������C=90����AC=2![]() ����BC�ij���
����BC�ij���
��2����ͼ2����ABC�У�DΪBC����һ�㣬BD=3��CD=1������AD����AC=2����֤����ABD�DZ��������Σ���������ȣ�
��3����ͼ3������ABCD�У���BADΪ�۽ǣ�PΪ�Խ���BD��һ���㣬��P��PH��CD��H����CP+PH��ֵ��Сʱ��APCDǡ������PDΪ�ı��������Σ��DZ���Ϊx��![]() =y����y����x�ĺ�����ϵʽ��
=y����y����x�ĺ�����ϵʽ��
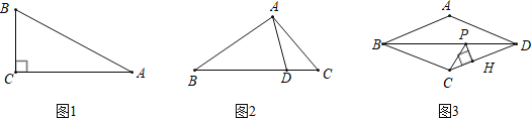
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӽס��ҡ�������ͬѧ�������ȡ����־Ը�ߣ��������¼��ĸ��ʣ�
��1����ȡ1����ǡ���Ǽף�
��2����ȡ2������������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com