
【题目】如图,在等腰Rt△ABC中,∠BAC=90°,BC=2,点P是△ABC内部的一个动点,且满足∠PBC=∠PCA,则线段AP长的最小值为( )
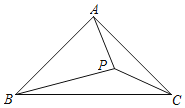
A.0.5B.![]() ﹣1C.2﹣
﹣1C.2﹣![]() D.
D.![]()
【答案】C
【解析】
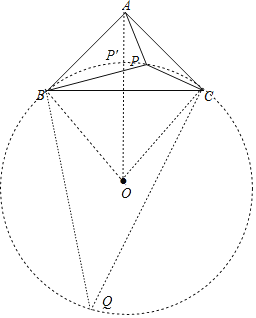
先计算出∠PBC+∠PCB=45°,则∠BPC=135°,利用圆周角定理可判断点P在以BC为弦的⊙O上,如图,连接OA交![]() 于P′,作
于P′,作![]() 所对的圆周角∠BQC,利用圆周角定理计算出∠BOC=90°,从而得到△OBC为等腰直角三角形,四边形ABOC为正方形,所以OA=BC=2,OB=
所对的圆周角∠BQC,利用圆周角定理计算出∠BOC=90°,从而得到△OBC为等腰直角三角形,四边形ABOC为正方形,所以OA=BC=2,OB=![]() ,根据三角形三边关系得到AP≥OA﹣OP(当且仅当A、P、O共线时取等号,即P点在P′位置),于是得到AP的最小值.
,根据三角形三边关系得到AP≥OA﹣OP(当且仅当A、P、O共线时取等号,即P点在P′位置),于是得到AP的最小值.
解:∵△ABC为等腰直角三角形,
∴∠ACB=45°,即∠PCB+∠PCA=45°,
∵∠PBC=∠PCA,
∴∠PBC+∠PCB=45°,
∴∠BPC=135°,
∴点P在以BC为弦的⊙O上,如图,连接OA交![]() 于P′,
于P′,
作![]() 所对的圆周角∠BQC,则∠BCQ=180°﹣∠BPC=45°,
所对的圆周角∠BQC,则∠BCQ=180°﹣∠BPC=45°,
∴∠BOC=2∠BQC=90°,
∴△OBC为等腰直角三角形,
∴四边形ABOC为正方形,
∴OA=BC=2,
∴OB=![]() BC=
BC=![]() ,
,
∵AP≥OA﹣OP(当且仅当A、P、O共线时取等号,即P点在P′位置),
∴AP的最小值为2﹣![]() .
.
故选:C.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图1,AB为半圆O的直径,半径OP⊥AB,过劣弧AP上一点D作DC⊥AB于点C.连接DB,交OP于点E,∠DBA=22.5°.
⑴ 若OC=2,则AC的长为 ;
⑵ 试写出AC与PE之间的数量关系,并说明理由;
⑶ 连接AD并延长,交OP的延长线于点G,设DC=x,GP=y,请求出x与y之间的等量关系式. (请先补全图形,再解答)
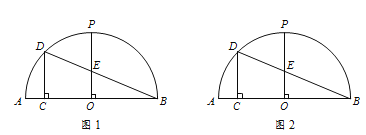
查看答案和解析>>
科目:初中数学 来源: 题型:
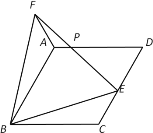
【题目】如图,在菱形ABCD中,∠ABC=60°,E是CD边上一点,作等边△BEF,连接AF.
(1)求证:CE=AF;
(2)EF与AD交于点P,∠DPE=48°,求∠CBE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )
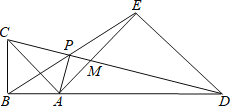
A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D(点P不与点A、B重合),作∠DPQ=60°,边PQ交射线DC于点Q.设点P的运动时间为t秒.
(1)用含t的代数式表示线段DC的长;
(2)当点Q与点C重合时,求t的值;
(3)设△PDQ与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式;
(4)当线段PQ的垂直平分线经过△ABC一边中点时,直接写出t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
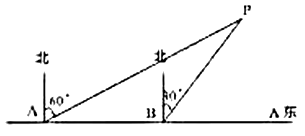
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明准备进行如下操作实验:把一根长为![]() 的铁丝剪成两段,并把每一段围成一个正方形.
的铁丝剪成两段,并把每一段围成一个正方形.
(1)要使这两个正方形的面积之和等于![]() ,小明该怎么剪?
,小明该怎么剪?
(2)小刚对小明说:“这两个正方形的面积之和不可能等于![]() .”小刚的说法对吗?请说明理由.
.”小刚的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(概念提出)如图 ①,若正△DEF的三个顶点分别在正△ABC的边AB、BC、AC上,则我们称△DEF是正△ABC的内接正三角形.
(1)求证:△ADF≌△BED.
(问题解决)利用直尺和圆规作正三角形的内接正三角形(保留作图痕迹,不写作法).
(2)如图 ②,正△ABC的边长为a,作正△ABC的内接正△DEF,使△DEF的边长最短,并说明理由;
(3)如图③,作正△ABC的内接正△DEF,使FD⊥AB.
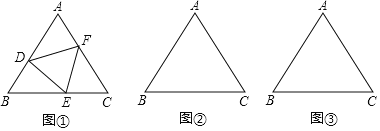
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() (
(![]() 为常数)经过抛物线
为常数)经过抛物线![]() 上的点
上的点![]() 及抛物线的顶点
及抛物线的顶点![]() .抛物线与
.抛物线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴的另一个交点为
轴的另一个交点为![]() .
.
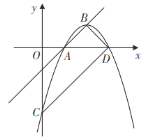
(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)根据图象,写出满足![]() 的
的![]() 的取值范围;
的取值范围;
(3)求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com