
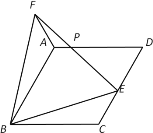
【题目】如图,在菱形ABCD中,∠ABC=60°,E是CD边上一点,作等边△BEF,连接AF.
(1)求证:CE=AF;
(2)EF与AD交于点P,∠DPE=48°,求∠CBE的度数.
【答案】(1)证明见解析(2)12°
【解析】
(1)根据菱形的性质,利用SAS判定△ABE≌△ADF,从而求得AE=AF
(2)根据菱形的性质,得出∠C的度数,利用三角形内角和180°的性质,得出∠DEP=72°,及∠CBE=∠BED-∠C的关系即可解答.
(1)证明:∵ 四边形ABCD是菱形,
∴ AB=BC.
∵ △BEF是等边三角形,
∴ BF=BE,∠FBE=∠FEB=60°.
∵ ∠ABC=60°,
∴ ∠ABC=∠FBE,
∴ ∠ABC-∠ABE=∠FBE-∠ABE,即∠EBC=∠FBA.
∴ △EBC≌△FBC(SAS).
∴ CE=AF.
(2)解:∵ 四边形ABCD是菱形,
∴ AD∥BC,∠D=∠ABC=60°.
∴ ∠C=180°-∠D=120°.
在△PDE中,∠D+∠DPE+∠PED=180°,
∴ ∠DEP=72°.
由(1)得,∠FEB=60°,
∴ ∠BED=∠DEP+∠BEP=72°+60°=132°.
∴ ∠CBE=∠BED-∠C=132°-120°=12°.


 能力评价系列答案
能力评价系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
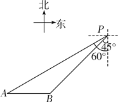
【题目】如图,一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项.现随机抽查了部分学生,并将其结果绘制成如下不完整的条形图和扇形图.
抽取的学生最喜欢体育活动的条形统计图
抽取的学生最喜欢体育活动的扇形统计图
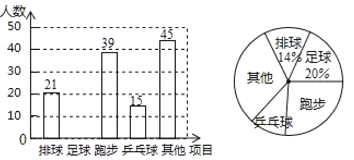
请结合以上信息解答下列问题:
(1)在这次调查中一共抽查了_____学生,扇形统计图中“乒乓球”所对应的圆心角为_____度,并请补全条形统计图;
(2)己知该校共有1200名学生,请你估计该校最喜爱跑步的学生人数;
(3)若在“排球、足球、跑步、乒乓球”四个活动项目任选两项设立课外兴趣小组,请用列表法或画树状图的方法求恰好选中“排球、乒乓球”这两项活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C三个城市位置如图所示,A城在B城正南方向180 km处,C城在B城南偏东37°方向.已知一列货车从A城出发匀速驶往B城,同时一辆客车从B城出发匀速驶往C城,出发1小时后,货车到达P地,客车到达M地,此时测得∠BPM=26°,两车又继续行驶1小时,货车到达Q地,客车到达N地,此时测得∠BNQ=45°,求两车的速度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin26°≈
,sin26°≈![]() ,cos26°≈
,cos26°≈![]() ,tan26°≈
,tan26°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级获得一个到高校体验的名额,从前期的选拔中,小明和小刚从众多报名者中脱颖而出:为公平起见,学校设计了如下的游戏:四张大小、质地相同的卡片上分别标有数字1、2、3、4.将标有数字的一面朝下,洗匀后从中抽取一张卡片,记下上面的数字,不放画,再从剩余的卡片中抽取一张卡片,记下上面的数字如果两次抽取卡片上数字之和是奇数,小明获胜:如果两次抽取卡片上数字之和是偶数,小刚获胜,获胜的同学将代表学校参加“高校体验”活动.请问:学校设计的这个游戏是否公平?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下统计图描述了九年级(1)班学生在为期一个月的读书月活动中,三个阶段(上旬、中旬、 下旬)日人均阅读时间的情况:
(1)从统计图可知,九年级(1)班共有学生多少人;
(2)求图22.1中a的值;
(3)从图22-1、22-2 中判断,在这次读书月活动中,该班学生每日阅读时间_______(填“普遍增加了”或“普遍减少了”);
(4)通过这次读书月活动,如果该班学生初步形成了良好的每日阅读习惯,参照以上统计图的变化趋势,至读书月活动结束时,该班学生日人均阅读时间在0.5~1(即0.5≤t<10)小 时的人数比活动开展初期增加了多少人.
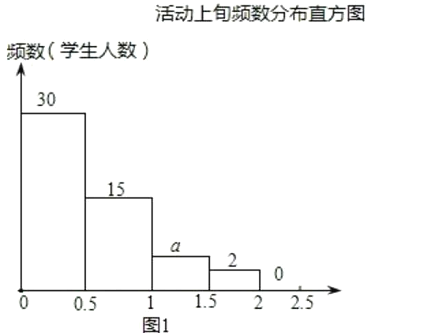


(每个小矩形含左端点,不含右端点) .
查看答案和解析>>
科目:初中数学 来源: 题型:
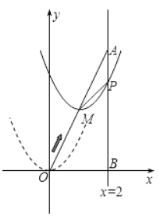
【题目】如图,在平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,连结
,连结![]() ,抛物线
,抛物线![]() 沿射线
沿射线![]() 方向平移得到抛物线
方向平移得到抛物线![]() ,抛物线
,抛物线![]() 与直线
与直线![]() 交于点
交于点![]() ,设抛物线
,设抛物线![]() 的顶点
的顶点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线![]() 的解析式(用含
的解析式(用含![]() 的式子表示);
的式子表示);
(2)连结![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)点![]() 为
为![]() 轴上的动点,以
轴上的动点,以![]() 为直角顶点的
为直角顶点的![]() 与
与![]() 相似,求
相似,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com