
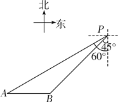
【题目】如图,一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
【答案】(10![]() +10)海里
+10)海里
【解析】
利用题意得到AC⊥PC,∠APC=60°,∠BPC=45°,AB=20海里,如图,设BC=x海里,则AC=AB+BC=(20+x)海里.解△PBC,得出PC=BC=x海里,解Rt△APC,得出AC=PCtan60°=![]() x,根据AC不变列出方程
x,根据AC不变列出方程![]() x=20+x,解方程即可.
x=20+x,解方程即可.
如图,AC⊥PC,∠APC=60°,∠BPC=45°,AB=20海里,设BC=x海里,则AC=AB+BC=(20+x)海里.
在△PBC中,∵∠BPC=45°,
∴△PBC为等腰直角三角形,
∴PC=BC=x海里,
在Rt△APC中,∵tan∠APC=![]() ,
,
∴AC=PCtan60°=![]() x,
x,
∴![]() x=20+x,
x=20+x,
解得x=10![]() +10,
+10,
则PC=(10![]() +10)海里.
+10)海里.
答:轮船航行途中与灯塔P的最短距离是(10![]() +10)海里.
+10)海里.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
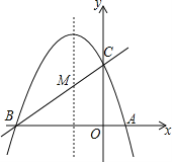
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
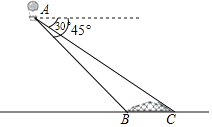
【题目】汉江是长江最长的支流,在历史上占居重要地位,陕西省境内的汉江为汉江上游段.李琳利用热气球探测器测量汉江某段河宽,如图,探测器在A处观测到正前方汉江两岸岸边的B、C两点,并测得B、C两点的俯角分别为45°,30°已知A处离地面的高度为80m,河平面BC与地面在同一水平面上,请你求出汉江该段河宽BC.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
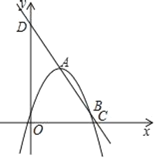
【题目】如图所示,二次函数y=k(x﹣1)2+2的图象与一次函数y=kx﹣k+2的图象交于A、B两点,点B在点A的右侧,直线AB分别与x、y轴交于C、D两点,其中k<0.
(1)求A、B两点的横坐标;
(2)若△OAB是以OA为腰的等腰三角形,求k的值;
(3)二次函数图象的对称轴与x轴交于点E,是否存在实数k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
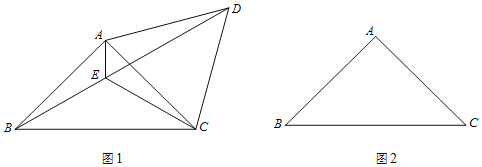
【题目】已知:在△ABC中,∠BAC=90°,AB=AC.
(1)如图1,将线段AC绕点A逆时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD于点E,连结CE.
①求证:∠AED=∠CED;
②用等式表示线段AE、CE、BD之间的数量关系(直接写出结果);
(2)在图2中,若将线段AC绕点A顺时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD的延长线于点E,连结CE.请补全图形,并用等式表示线段AE、CE、BD之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
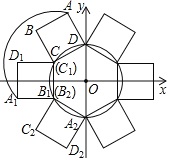
【题目】如图,⊙O的半径为2,圆心O在坐标原点,正方形ABCD的边长为2,点A、B在第二象限,点C、D在⊙O上,且点D的坐标为(0,2),现将正方形ABCD绕点C按逆时针方向旋转150°,点B运动到了⊙O上点B1处,点A、D分别运动到了点A1、D1处,即得到正方形A1B1C1D1(点C1与C重合);再将正方形A1B1C1D1绕点B1按逆时针方向旋转150°,点A1运动到了⊙O上点A2处,点D1、C1分别运动到了点D2、C2处,即得到正方形A2B2C2D2(点B2与B1重合),…,按上述方法旋转2020次后,点A2020的坐标为( )
A.(0,2)B.(2+![]() ,﹣1)
,﹣1)
C.(﹣1﹣![]() ,﹣1﹣
,﹣1﹣![]() )D.(1,﹣2﹣
)D.(1,﹣2﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
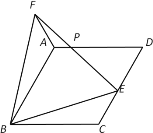
【题目】如图,在菱形ABCD中,∠ABC=60°,E是CD边上一点,作等边△BEF,连接AF.
(1)求证:CE=AF;
(2)EF与AD交于点P,∠DPE=48°,求∠CBE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
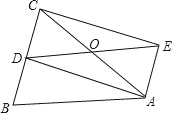
【题目】如图,在△ABC中,AB=AC,D为BC的中点,四边形ABDE是平行四边形.
(1)求证:四边形ADCE是矩形;
(2)若AC、DE交于点O,四边形ADCE的面积为16![]() ,CD=4,求∠AOD的度数.
,CD=4,求∠AOD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com